Two point charge Q and 4Q are fixed at a distance of 12cm from each other. Sketch lines of force and locate the neutral point, if any .
Step-by-Step Solution
1. Identify the Charges and Distance:
We have two point charges, Q and 4Q, fixed at a distance of 12 cm from each other.
2. Understanding Electric Field Direction:
Since both charges are positive, the electric field lines will originate from both charges and point away from them. The electric field due to charge Q will point away from Q, and the electric field due to charge 4Q will point away from 4Q.
3. Locate the Neutral Point:
The neutral point is where the net electric field due to both charges is zero. This occurs when the electric field produced by Q is equal in magnitude but opposite in direction to the electric field produced by 4Q.
4. Setting Up the Equation:
Let’s denote the distance from charge Q to the neutral point as x. Therefore, the distance from charge 4Q to the neutral point will be 12−x.
The electric field E1 due to charge Q at the neutral point is given by:
E1=kQx2
The electric field E2 due to charge 4Q is given by:
E2=k⋅4Q(12−x)2
5. Equating the Electric Fields:
For the neutral point, we set E1=E2:
kQx2=k⋅4Q(12−x)2
We can cancel k and Q from both sides:
1x2=4(12−x)2
6. Cross-Multiplying:
Cross-multiplying gives:
(12−x)2=4x2
7. Expanding and Rearranging:
Expanding the left side:
144−24x+x2=4x2
Rearranging gives:
3x2−24x+144=0
8. Simplifying the Quadratic Equation:
Dividing the entire equation by 3:
x2−8x+48=0
9. Using the Quadratic Formula:
We can use the quadratic formula x=−b±√b2−4ac2a:
x=8±√(−8)2−4⋅1⋅482⋅1
x=8±√64−1922
x=8±√−1282
Since the discriminant is negative, we conclude that there is no neutral point between the charges.
10. Sketching the Lines of Force:
- Draw two positive charges, Q and 4Q.
- Draw electric field lines originating from both charges, with more lines emanating from 4Q since it has a greater magnitude.
- Ensure that the lines do not intersect and that they extend outward towards infinity.
We have two point charges, Q and 4Q, fixed at a distance of 12 cm from each other.
Since both charges are positive, the electric field lines will originate from both charges and point away from them. The electric field due to charge Q will point away from Q, and the electric field due to charge 4Q will point away from 4Q.
The neutral point is where the net electric field due to both charges is zero. This occurs when the electric field produced by Q is equal in magnitude but opposite in direction to the electric field produced by 4Q.
Let’s denote the distance from charge Q to the neutral point as x. Therefore, the distance from charge 4Q to the neutral point will be 12−x.
E1=kQx2
The electric field E2 due to charge 4Q is given by:
E2=k⋅4Q(12−x)2
For the neutral point, we set E1=E2:
kQx2=k⋅4Q(12−x)2
We can cancel k and Q from both sides:
1x2=4(12−x)2
Cross-multiplying gives:
(12−x)2=4x2
Expanding the left side:
144−24x+x2=4x2
Rearranging gives:
3x2−24x+144=0
Dividing the entire equation by 3:
x2−8x+48=0
We can use the quadratic formula x=−b±√b2−4ac2a:
x=8±√(−8)2−4⋅1⋅482⋅1
x=8±√64−1922
x=8±√−1282
Since the discriminant is negative, we conclude that there is no neutral point between the charges.
- Draw two positive charges, Q and 4Q.
- Draw electric field lines originating from both charges, with more lines emanating from 4Q since it has a greater magnitude.
- Ensure that the lines do not intersect and that they extend outward towards infinity.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two point charges Q and -Q/4 are separated by a distance x.

View SolutionTwo points charges q1andq2 are placed at a distance of 50 m from each each other in air, and interact with a certain force. The same charges are now put in oil whose relative permittivity is 5. If the interacting force between them is still the same, their separation now is
View SolutionTwo idential point charges Q are kept at a distance r from each other. A third point charge is placed on the line joing the above two charges such that all the three charges are in equilibrium. The third charge
(a) should be of magnitude q=………..
(b) should be of sign .......
(c ) should be placed ........ .
View SolutionTwo point charges Q1 and Q2 lie along a line at a distance from each other. Figure 3.7 shows the potential variation along the line of charges. At which of the points 1, 2, and 3 is the electric field zero ? What are the singns of the charges Q1 and Q2 and which of the two charges is greater in magnitude ?
 .
.
View SolutionA charge Q is fixed at a distance d in front of an infinite metal plate. The lines of force are represented by

View SolutionTwo point electric charges of value q and 2q are kept at a distance d apart from each other in air. A third charge Q is to be kept along the same line in such a way that the net force action on q and 2q is zero. Calculate the position of charge Q in terms of q and d.
View SolutionTwo point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
View SolutionThe point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
View SolutionTwo spherical , nonconducting and very tin shells of uniformly distributed positive charge Q and radius d are located a distance 10d from each other . A positive point charge q is placed inside one of the shells at a distance d/2 from the center, on the line connecting the centers of the two shells , as shown in the figure, What is the net force on the charge q ? .
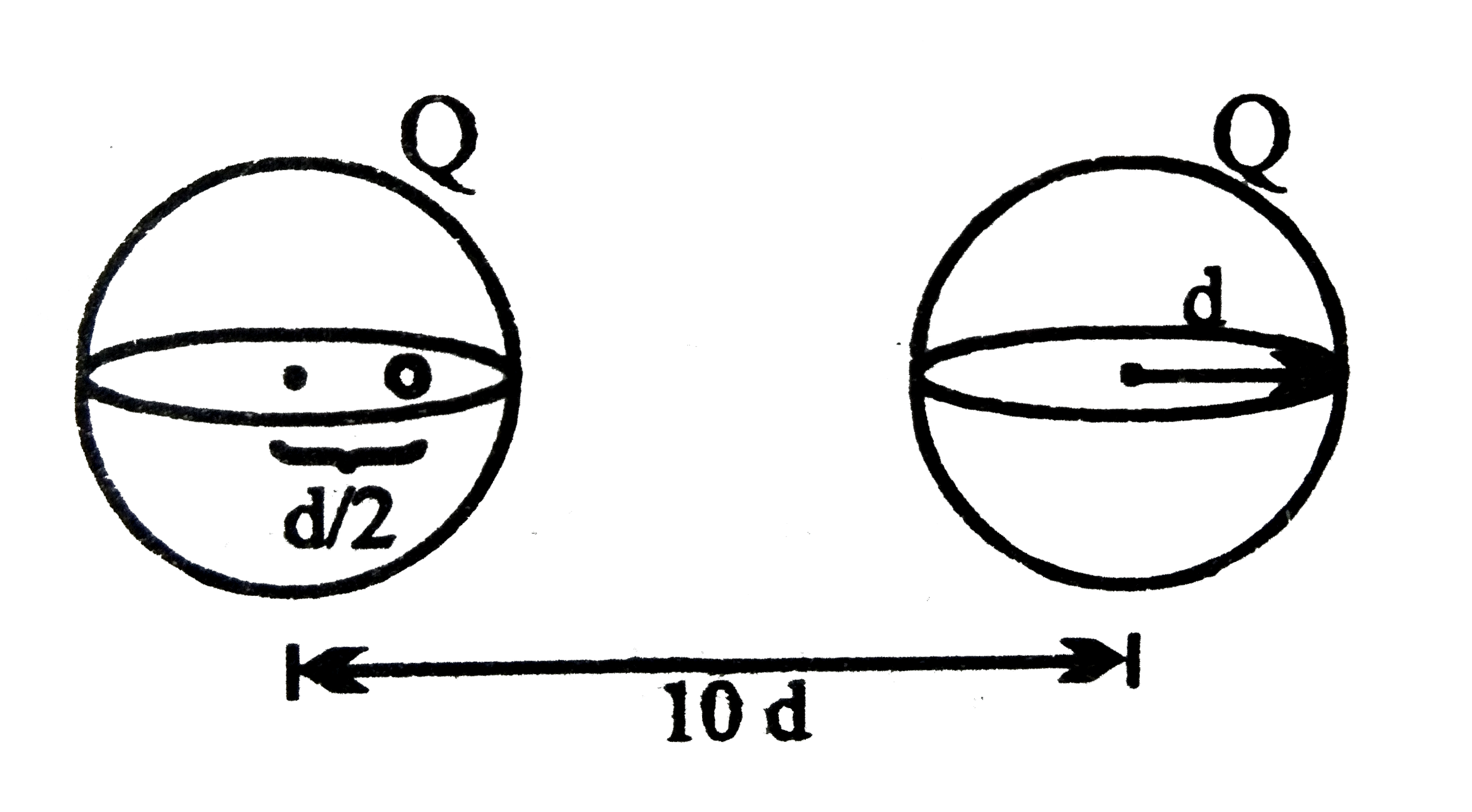
View SolutionTwo free point charges +qand+4q are placed apart a distance x. A third charge is so placed that all the three charges are in equilibrium. Then
View Solution
