A thin uniform square plate ABCD of side a and mass m is suspended in a vertical plane as shown in the figure. AE and BF are two massless inextensible strings. The line AB is horizontal. The tension in AE just after BF is cut will be

(a)2mg5
(b)mg
(c)2mg7
(d)3mg5
The correct Answer is:A
Let a0 be the acceleration of centre G and α be the angular acceleration of the plate just after cutting the string BF.
mg−T=ma0……..i
τG=IGα⇒Ta2=ma26α
⇒T=maα3…………iii

Just after cutting BF, net acceleration of A is resultant of two acceleration a0andαa/√2 as shown. But the net acceleration of A in the vertical direction should be zero.
Hence, a0=αa√2sin45∘
⇒a0=αa2.............ii
From eqn i , ii and iii we get
T=2mg5
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
A uniform square plate of mass m is supported with its plane vertical as shown in the figure. Assume the centre of mass is on a horizontal the passing through A. If the cable at B breaks then just after that the angular acceleration of the plate is
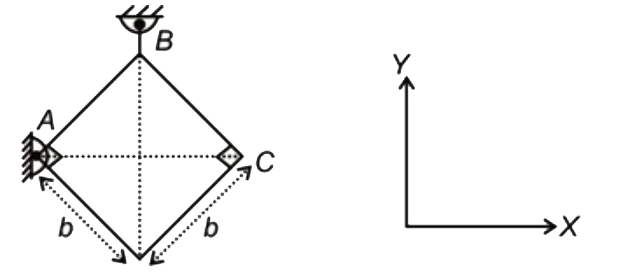
View SolutionA uniform triangular plate ABCof moment of mass m and inertia I (about an axis passing through A and perpendicular to plane of the plate) can rotate freely in the vertical plane about point 'A' as shown in figure. The plate is released from the position shown in the figure. Line AB is horizontal. The acceleration of centre of mass just after the release of plate is

View Solution
Knowledge Check
A mass M of 100 kg is suspended with the use of strings A, B 90 and C as shown in the figure, where W is the vertical wall and R is a rigid horizontal rod. The tension in the string B is
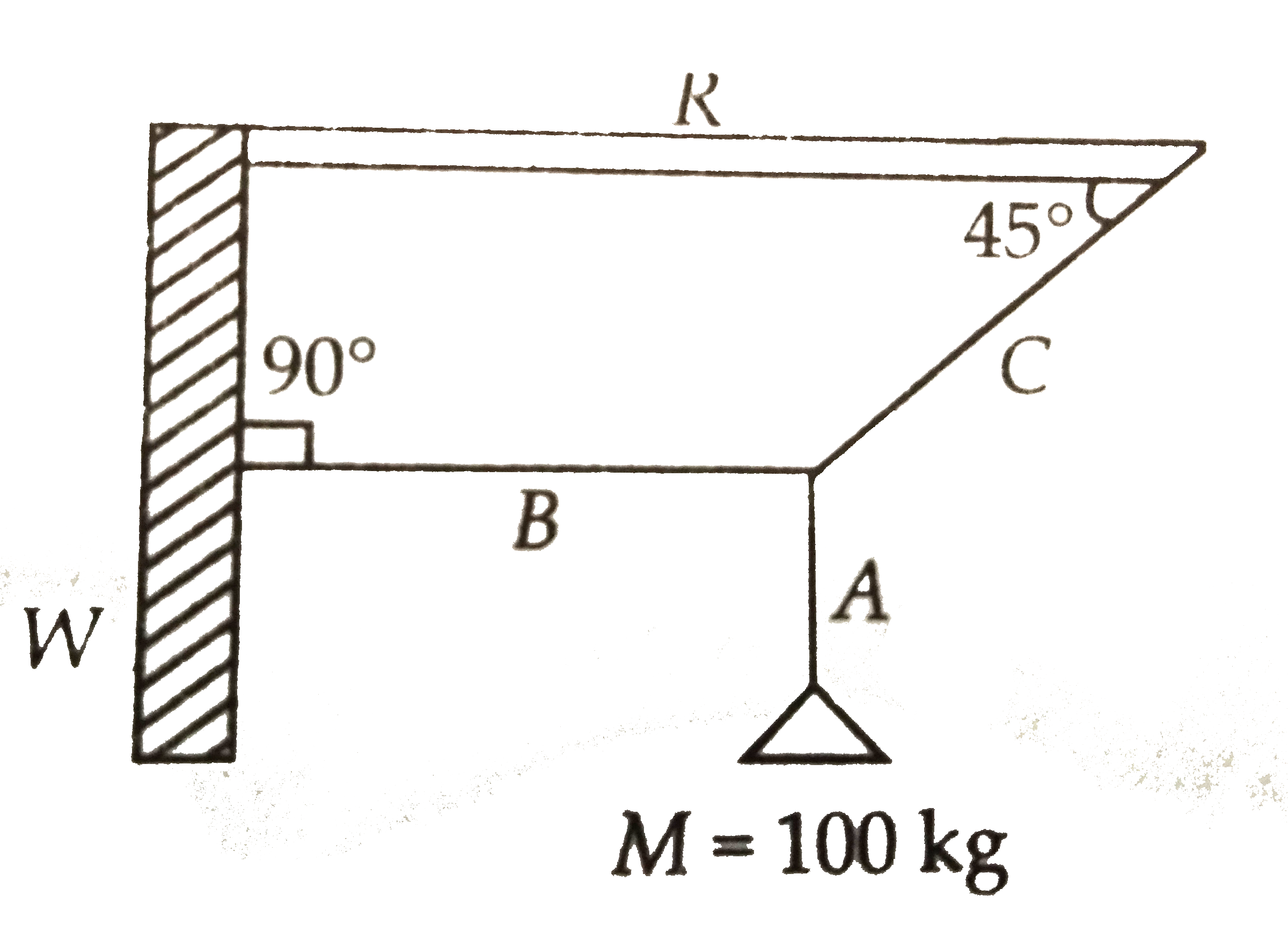 A100g NBzeroC100√2gND100√2gN
A100g NBzeroC100√2gND100√2gN
A uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

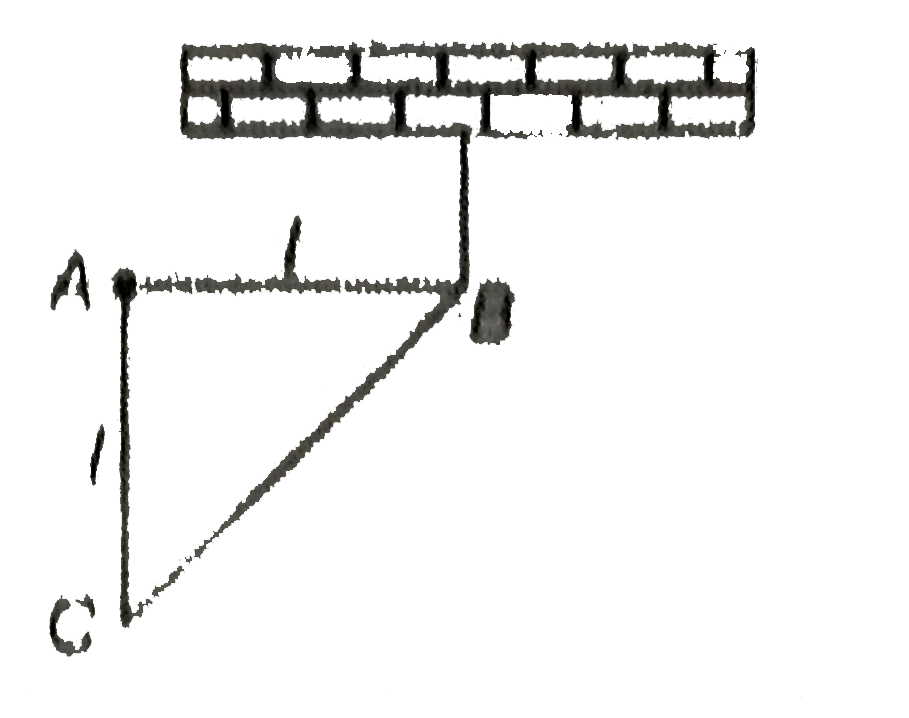
View SolutionA right triangular plate ABC of mass m is free to rotate in the verticle plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is
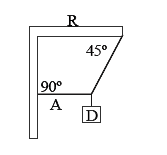
View SolutionA blolck D weighing 300kg is suspended by means of two cords A and B as shown in the figure. W is a vertical wall and R a horizontal rigid beam. The tension in the string A in kg is :
View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is

View SolutionA uniform rod length is l hinged at A and suspended with vertical string as shown in figure it string is cut then acceleration of centre of mass at this instant will be (g=10ms2)
View Solution
