A ring of mass 3kg is rolling Without Slipping with linear velocity 1ms−1 on a smooth horizontal surface. A rod of same mass is fitted along its one diameter. Find total kinetic energy of the system (in J).
The correct Answer is:5
To find the total kinetic energy of the system consisting of a ring and a rod, we need to consider both the translational and rotational kinetic energies.
Step 1: Identify the components of kinetic energy
The total kinetic energy (KE) of the system will be the sum of the translational kinetic energy (TKE) and the rotational kinetic energy (RKE).
Step 2: Calculate the translational kinetic energy
The translational kinetic energy for the system is given by the formula:
TKE=12mv2
where:
- m is the total mass of the system,
- v is the linear velocity.
Since both the ring and the rod have the same mass of 3kg, the total mass m is:
m=3kg+3kg=6kg
Substituting the values:
TKE=12×6kg×(1m/s)2=12×6×1=3J
Step 3: Calculate the moment of inertia of the system
The moment of inertia I of the ring about its center is:
Iring=mr2=3kg⋅r2
The moment of inertia I of the rod about its end (using the parallel axis theorem) is:
Irod=13mr2=13⋅3kg⋅r2=r2
Thus, the total moment of inertia Itotal is:
Itotal=Iring+Irod=3r2+r2=4r2
Step 4: Calculate the rotational kinetic energy
The rotational kinetic energy is given by:
RKE=12Iω2
We know that ω can be related to v by the equation v=rω, which gives:
ω=vr
Substituting this into the RKE formula:
RKE=12(4r2)(vr)2=12(4r2)(1r2)=2J
Step 5: Calculate the total kinetic energy
Now, we can find the total kinetic energy of the system:
Total KE=TKE+RKE=3J+2J=5J
Final Answer
The total kinetic energy of the system is 5J.
---
The total kinetic energy (KE) of the system will be the sum of the translational kinetic energy (TKE) and the rotational kinetic energy (RKE).
The translational kinetic energy for the system is given by the formula:
TKE=12mv2
where:
- m is the total mass of the system,
- v is the linear velocity.
m=3kg+3kg=6kg
Substituting the values:
TKE=12×6kg×(1m/s)2=12×6×1=3J
The moment of inertia I of the ring about its center is:
Iring=mr2=3kg⋅r2
The moment of inertia I of the rod about its end (using the parallel axis theorem) is:
Irod=13mr2=13⋅3kg⋅r2=r2
Thus, the total moment of inertia Itotal is:
Itotal=Iring+Irod=3r2+r2=4r2
The rotational kinetic energy is given by:
RKE=12Iω2
We know that ω can be related to v by the equation v=rω, which gives:
ω=vr
Substituting this into the RKE formula:
RKE=12(4r2)(vr)2=12(4r2)(1r2)=2J
Now, we can find the total kinetic energy of the system:
Total KE=TKE+RKE=3J+2J=5J
The total kinetic energy of the system is 5J.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False
4 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A ring of mass m is rolling without slipping with linear velocity v as shown is figure. A rod of identical mass is fixed alone one of its diameter. The total kinetic energy of the system is
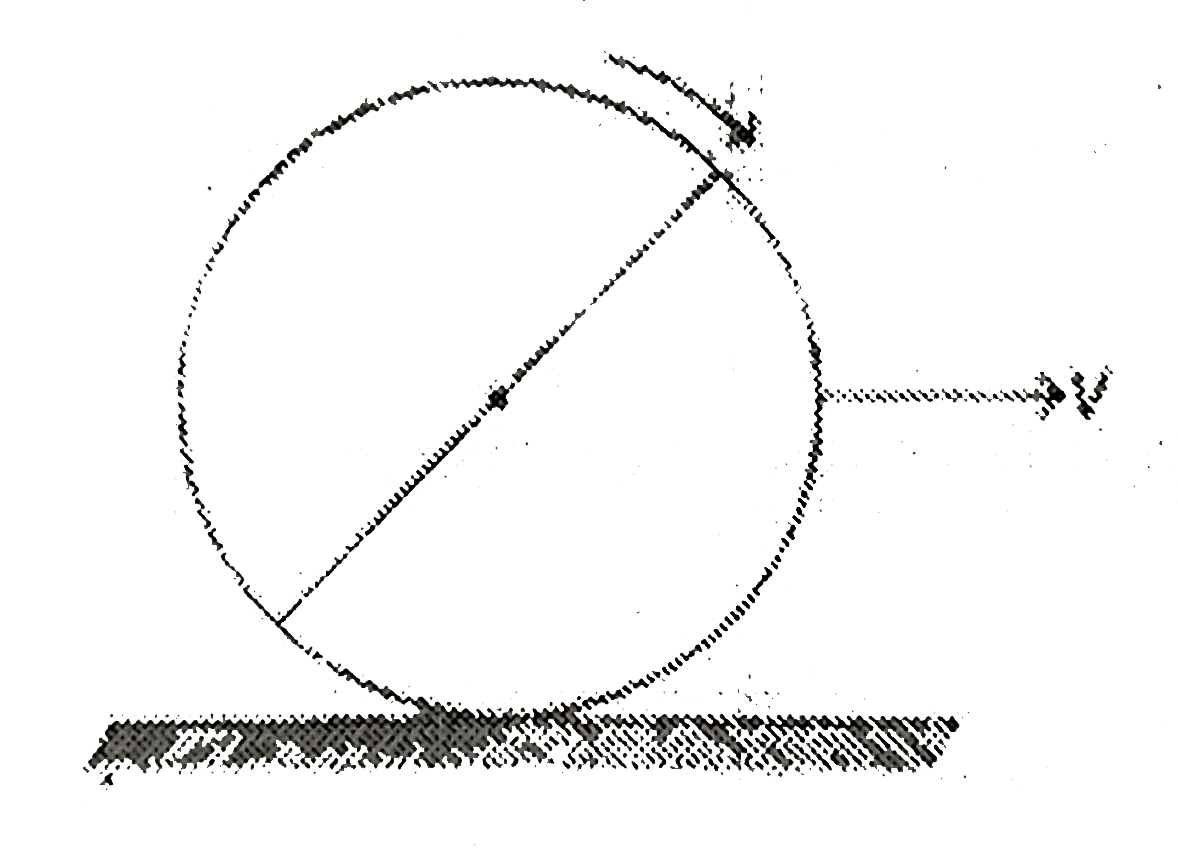
View Solution
A ring of mass m is rolling without slipping with linear speed v as shown in figure. Four particles each of mass m are also attached at points A, B , C and D find total kinetic energy of the system.
View Solution
Knowledge Check
A wheel of mass 5kg and radius 0.40m is rolling on a road without sliding with angular velocity 10rads−1. The moment of ineria of the wheel about the axis of rotation is 0.65kgm2. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
A22.4%B11.2%C88.8%D44.8%
In the figure shown, a ring A is initially rolling without sliding with a velocity 1, on the horizontal surface of the body B (of same mass as A). All surfaces arc smooth. B has no initial velocity. What will be the maximum height reached by A on B?

View SolutionA small sphere of mass 1 kg is rolling without slipping with linear speed
v=√2007m/s

It leaves the inclined plane at point C.
Find ratio of rotational and translational kinetic energy of the sphere when it strikes the ground after leaving from point C.
View SolutionA solid sphere rolls on horizontal surface without slipping. What is the ratio of its rotational to translation kinetic energy.
View SolutionA sphere of mass 50 gm and diameter 2 cm rolls without slipping with a velocfty of 5 cm/s. Calculate the total energy.
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View SolutionA uniform thin spherical shell of mass m and radius R rolls down without slipping over an inclined plane of angle θ with the horizontal. The ratio of rotational kinetic energy to the total kinetic energy of the shell will be
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View Solution
