A sphere of mass M and radius are shown in figure slips on a rough horizontal plane. At some instant it has translational velocity v0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
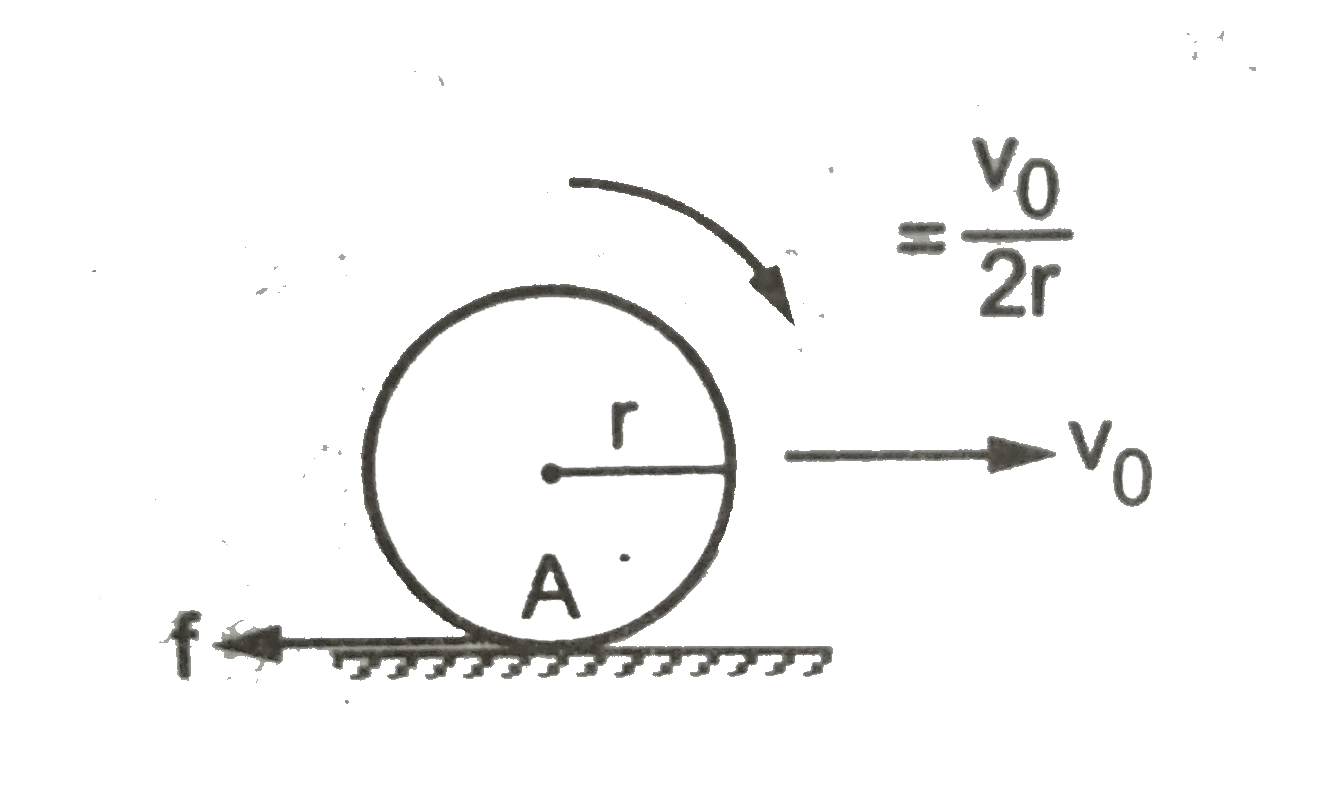
Velcity of the centre =v0 and the angular velocity about the centre =v0/2r. Thus v0>ω0r. The sphere slips forward and thus the firction by the plane on the sphere will act backward. As the firction is kinetic, its value is μ=μMg and the sphere wil be decelerated by aCM=fM
Hence,v(t)=v0−fMt...........i
This friction will also have a torque = about the centre. this torque is clockwise and in the direction of ω0. Hence, the angular acceleration about the centre will be
α=fr(25)Mr2=5f2Mr
=v02r+52Mrt
Pure rolling starts when v(t)=rω(t),
i.e, v(t)=v02+5f2Mt ............ii
Eliminating t from eqn i and ii we get
52v(t)+v(t)=52v0+v02
or v(t)=27×3v0=67v0
Thus, the sphere rolls with translational velocity 6v0/7 in the forward direction.
Alternative method: We can solve this problem by using conservation of angular momentum. We can conserve the angular momentum about any point situated on the ground. (as torque of friction for about any point on the ground is Zero).
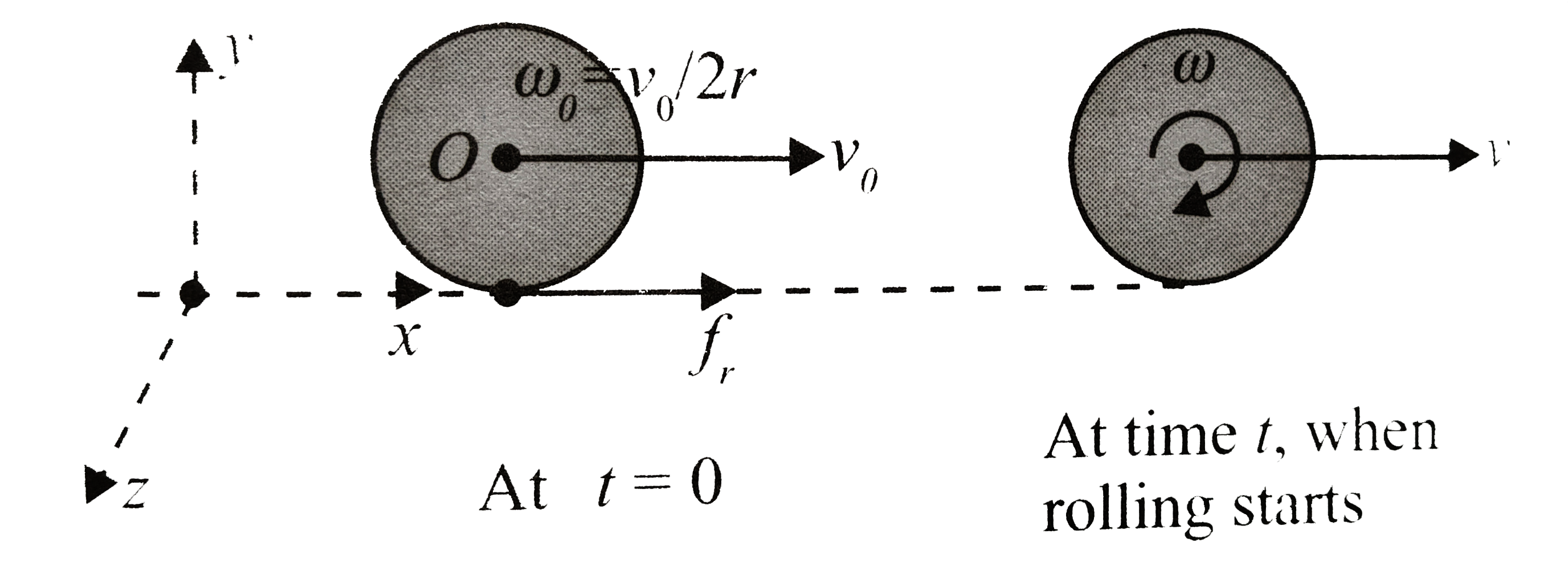
Angular momentum about any point O situated on ground at t=0
→Linitial=→LCM+→r×m→v
=ICMω−ˆk+Mv0r(−ˆk)
=[25Mr2(v02r)+Mv0r](−ˆk)
→Linitial=65Mv0(−ˆk)..........i
Angular momentum at time t when rolling starts
→Lfinal=→Lcm+→r×m→v=25mr2ω(−ˆk)+mvr(−ˆk)
When rolling startsv=ωR or ω=vr
Hence →Lfinal=[25mr2(vr)+mvr](−ˆk)
=75mvr(−ˆk)........ii
Conserving angular momentum we get
→Linitial=→Lfinal
65mv0r(−ˆk)=75mvr(−ˆk)
which gives v=67v0
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
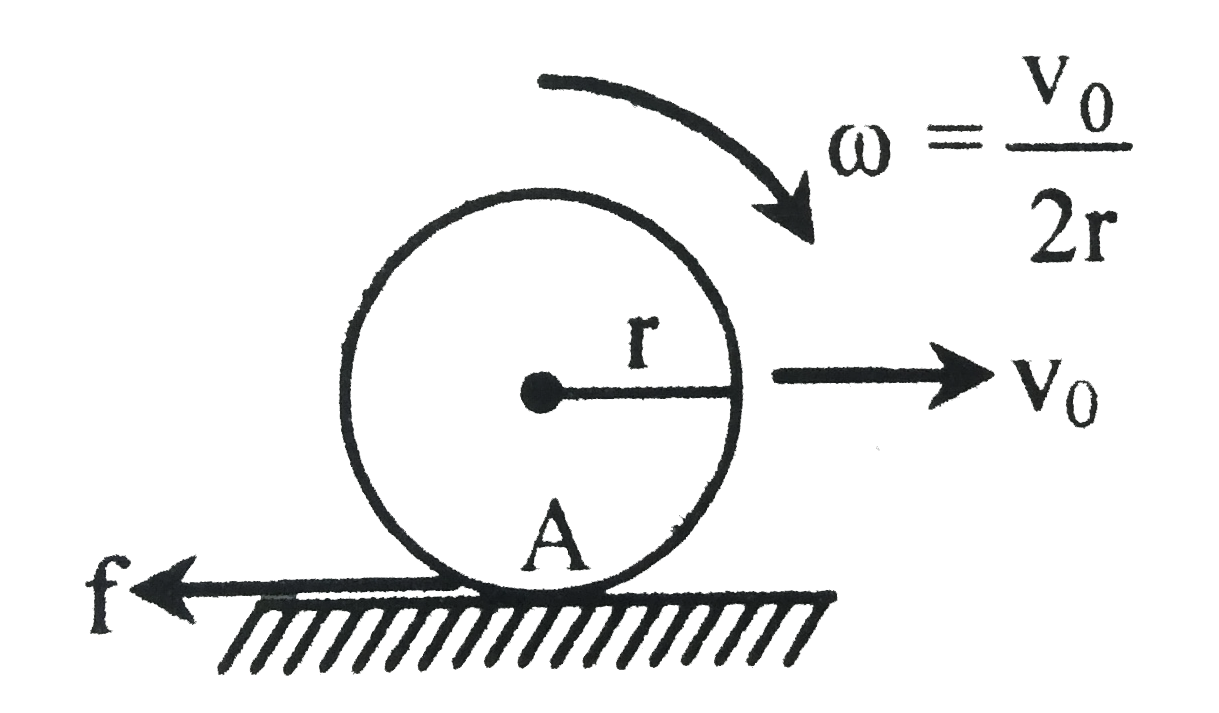 .
.
View SolutionA sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v0, and rotational velocity about centre v0/2r. The percentage change of translational velocity after the sphere start pure rolling:

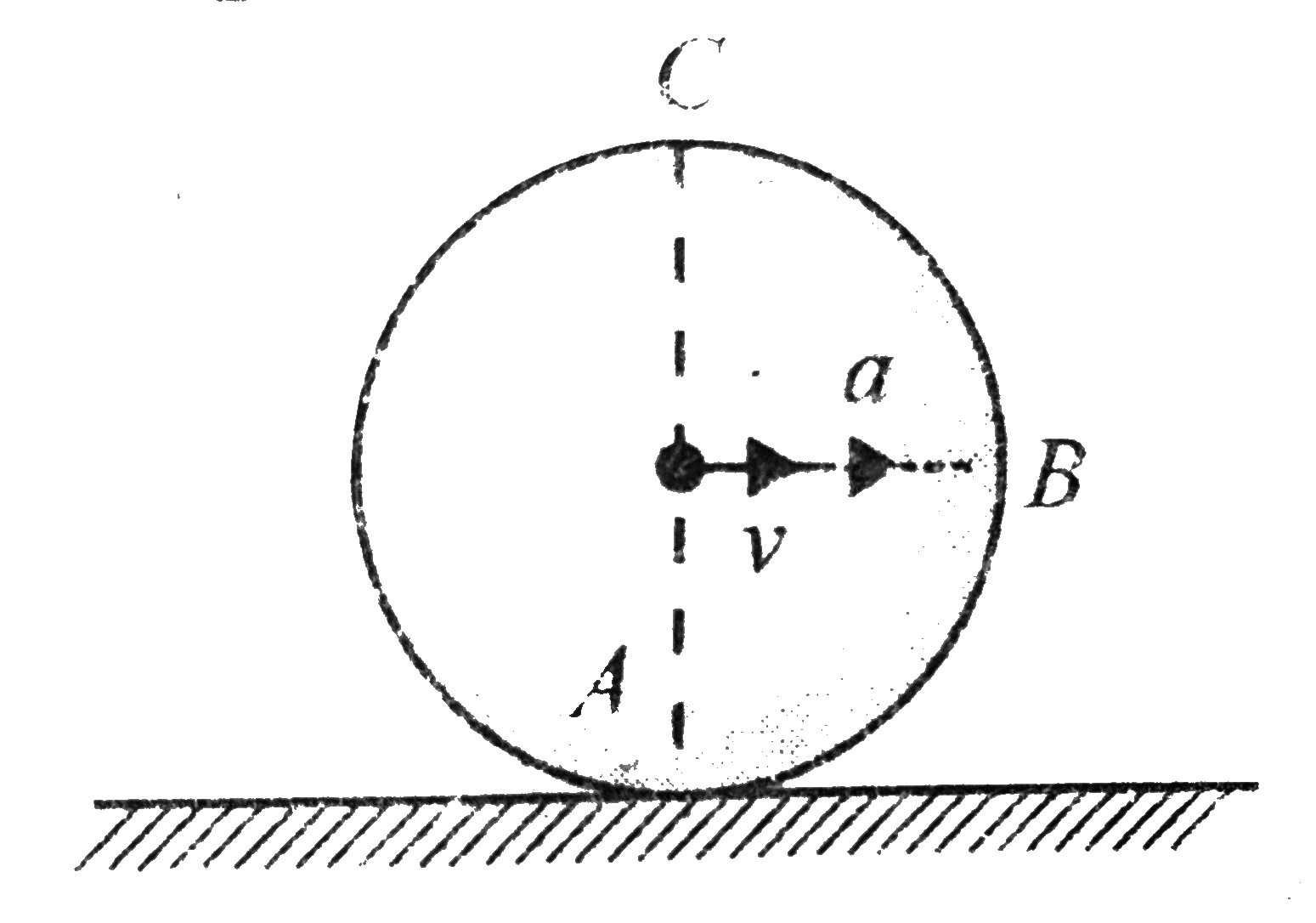
View SolutionA wheel is rolling on a horizontal plane. At a certain instant it has a velocity v and acceleration a of CM as shown in figure . Acceleration of
View SolutionA solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is
View SolutionA solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA solid sphere of mass M and radius R is in pure rolling as shown in figure. The angular momentum of the sphere about the origin is (linear velocity of centre of mass is v0, in positive x-direction)
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
View Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
View Solution