A cylinder of height H and diameter H/4 is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is 2H from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
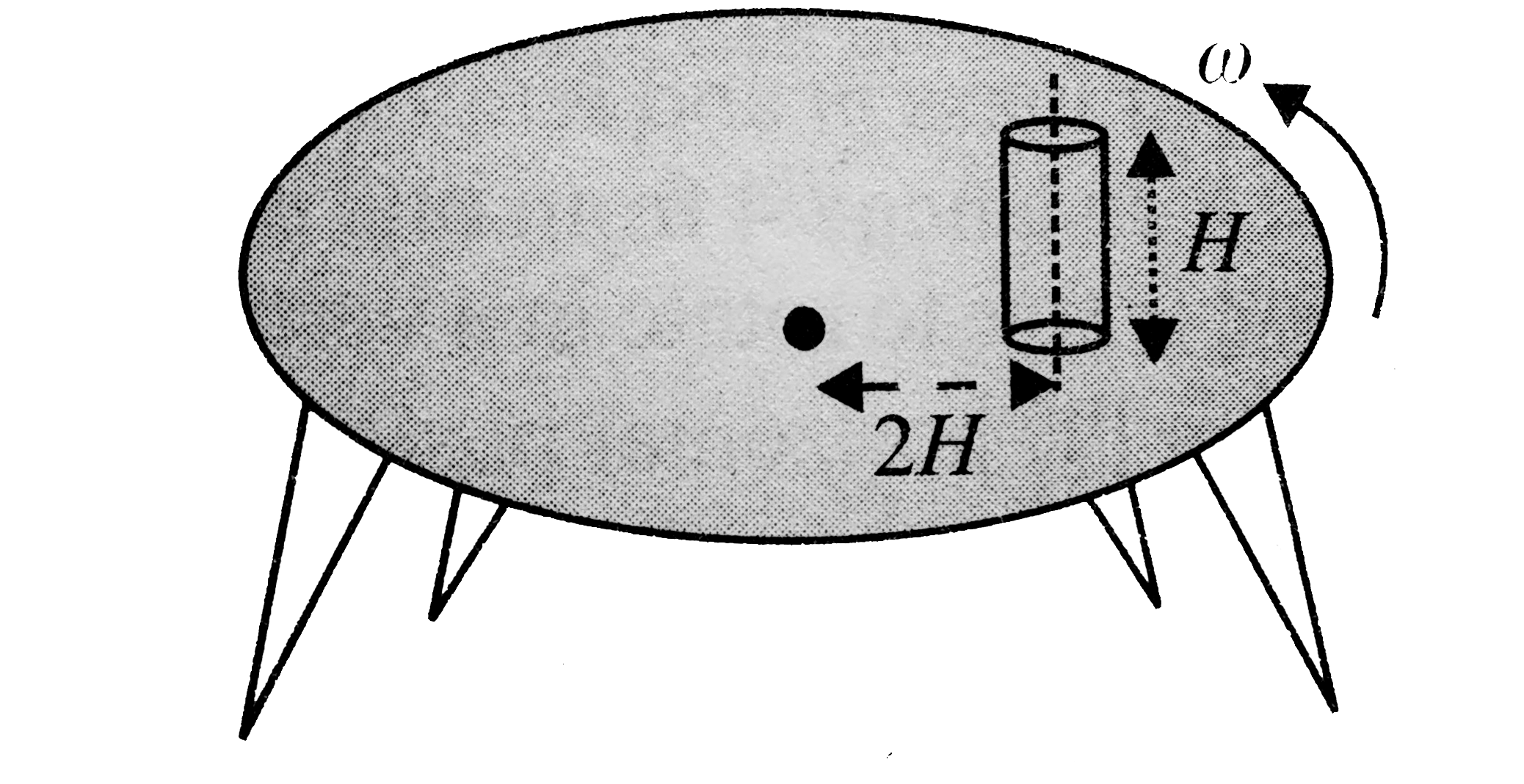
√g2(12−H)
√g(12−H)
√g4H
√g8H
The correct Answer is:D
N=mg ……i
Net moment of all force about point P is zero. FH2=mgh.8,ω=√g8H

Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View SolutionA cylinder of radius R and height H is foam unknown height h. When is rotated at an unknown constant angular velocity ω, the base of the cylinder gets exposed when the liquid just starts spilling out, as shown in Fig.
a. Find the height h of the liquid.
b. Find the angular speed w of the cylinder.

View Solution
Knowledge Check
A cylinder has volume V, height h, and base diameter d. Which of the following represents d in terms of V and h?
Ad=√VπhBd=√vπhCd=√2VπhDd=√4Vπh
A cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.

View SolutionA cylinder of weight W and radius R is to be raised onto a horizontal step of height h as shown in Fig. A rope is wrapped around the cylinder and pulled horizontally with force F. Assuming the cylinder does not slip on the step, find the minimum force F necessary to raise the cylinder.

View SolutionA small body of mass 100 g moving with a velocity 2 m/s is strikes a solid cylinder of mass 2 kg and radius 20 cm. The cylinder is initially at rest and is mounted on a fixed horizontal axle that passes through the centre of mass. The line of motion of the small body is at a perpendicular lar distance of 15 cm from the centre of the cylinder. The small body strikes the cylinder and adheres to its surface. What is the angular speed of the system just after the collision ? Assume there is no friction.
View SolutionA block of mass m height 2h and width 2b rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is μ.
b. the value of the acceleration at which block topples about A, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of 20ms−1 with constant deceleration so that the block is not disturbed. The following data are given b=0.6m,h=0.9m,μ=0.5 and g=10ms−2
View SolutionA cylinder of mass M and radius R is to be raised on a horizontal step of height h=R3. Cylinder is pulled by a rope as shown in figure. Assuming no slipping, the minimum value of force F to raise the cylinder is
_PHY_E05_246_Q01.png)
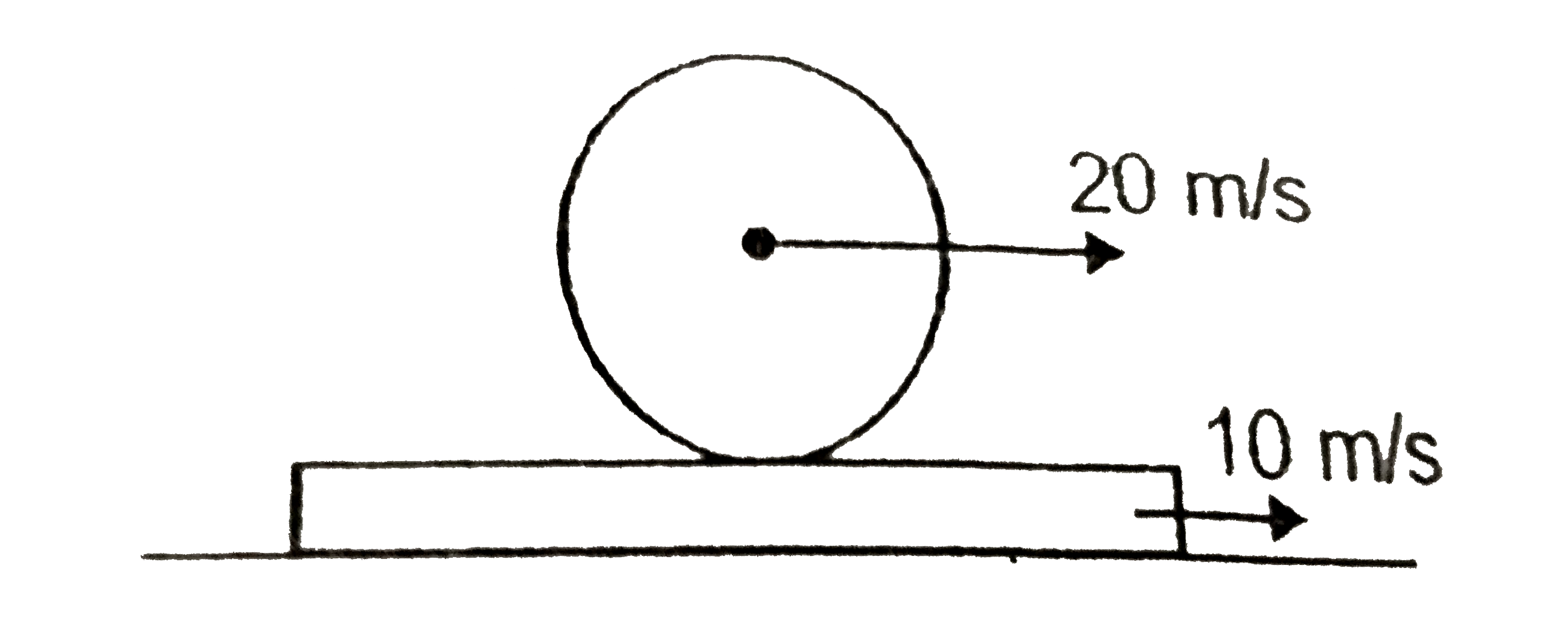
View SolutionA cylinder is rolling without slipping on a plank which is also moving with speed 10m/s on a horizontal surface as shown. The speed of centre of the cylinder is 20m/s. The mass of cylinder is 2kg. The kinetic energy of the cylinder when observed from ground is
View SolutionA solid cylinder with r=0.1m and mass M=2kg is placed such that it is in contact with the vertical and a horizontal surface as shown in Fig. The coefficient of friction is μ=(1/3) for both the surfaces. Find the distance (in CM) from the centre of the cylinder at .which a force F=40N should be applied vertically so that the cylinder just starts rotating in anticlockwise direction.

View Solution
