Four identical rods, each of mass and length , make a square frame in the plane as shown in Fig.
a. Calculate its moment of inertia about the -and y-axes.
b. Also, calculate its moment of inertia about the -axis.

a. Due to symmetry the moment of inertia of the square frame about the - and -axes are equal i.e.,
Now
b. Due to perpendicular axis theorem
Note that the -axis does not pass through its centre of mass.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.3
15 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Calculate the moment of inertia of the given rod about an axis CD.
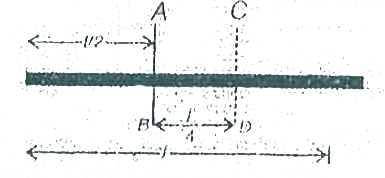
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertia about
View SolutionA thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be :
View SolutionCalculate the moment of inertia of the given rod about an axis CD

View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionCalculate the moment of inertia of each particle in Fig. about the indicated axis of rotation.

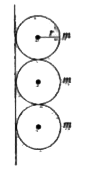
View SolutionThree identical rings of masses m each and radius r are kept in contact as shown in Fig. Find the moment of inertia of the system about a common tangent.
View Solution
