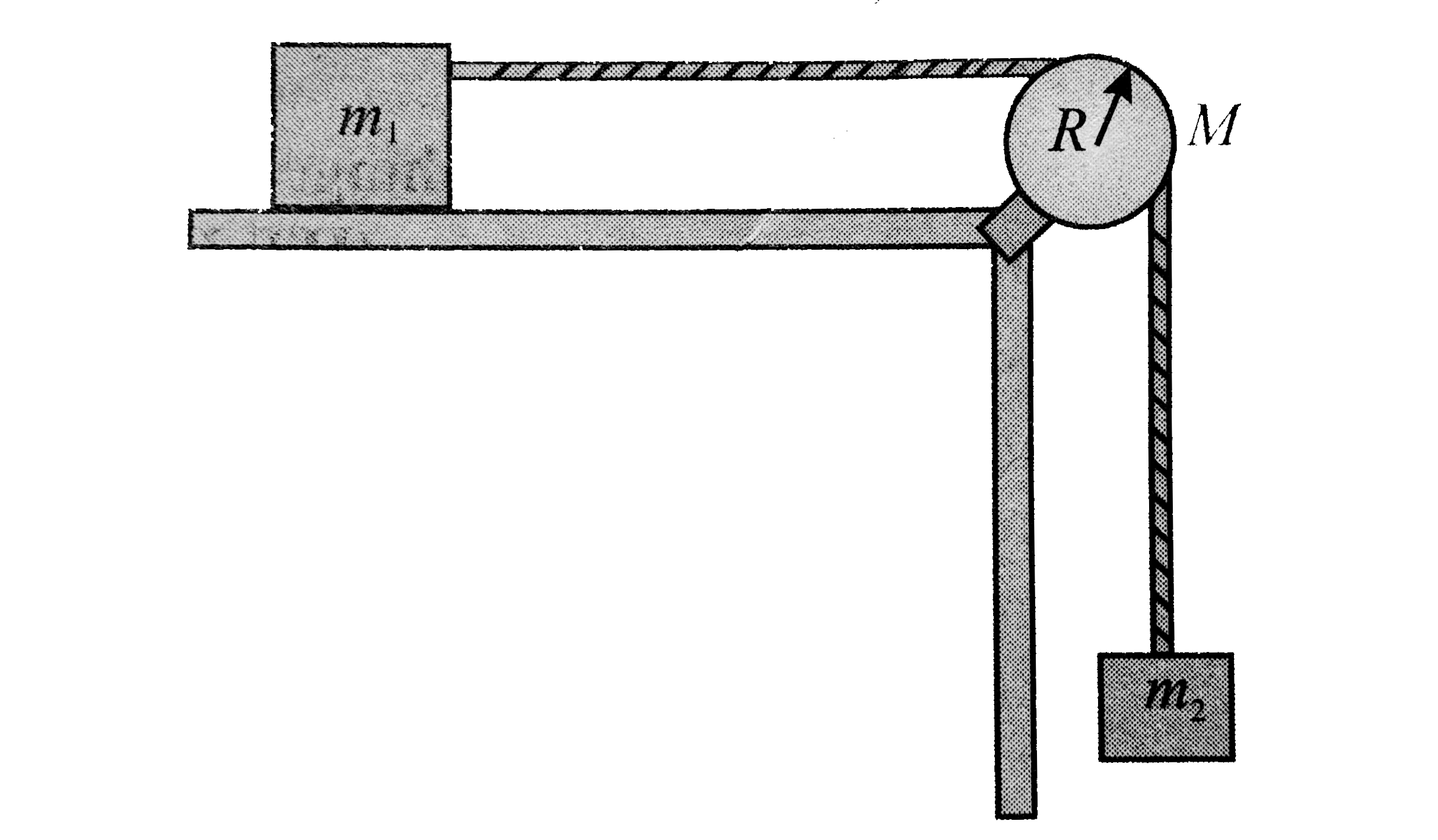
In figure mass m1 slides without friction on the horizontal surface, the frictionless pulley is in the form of a cylinder of mass M and radius R, and a string turns the pulley without slipping. Find the acceleration of each mass, and tension in each part of the string.
Through this illustration we will learn the application of torque equation and constraint relation in more complex case here. We have change the block with cylinder M2 Pulley M1 will have oly pure rotation while cylinder M2 will have rotatioin and translation combined. Let us analyse step by step in the same way as the previous illustration.
Step I: Analyse the motion of the pulley and the cyinder. Pulley: One rotational acceleration α1 (clockwise)
Cylinder: One rotational acceleration α2 (clockwise) andn a linear acceleration a2 (downward)
Step II: Equation of motion for M2
M2g−T=M2a2 ..........i
Step III: Torque equation for pulley τc=Icα
TR=(M1R22)α1⇒2TM1R.......ii
Torquue equation for the cylinder (about centre of mass of cylinder τc=Icα
⇒TR=(M2R22)α2
α2=2TM2R.........iii
Step IV: The acceleration of P and Q should be equal as both are connected with the same inextensible string ltbr> Accceleration of P,aM=α1R (downward) .........iv
Acceleration of Q,aN=a2−α2R (downwards) .............. v
Hence, constraint relation α1R=a2−α2R .............vi
Step V: Solving equations
After solving eqn i, ii, iii and iv, we get
a2=[(2M1+M2)3M1+2M2]g
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The strings are inextensible and light: the pulleys are smooth and light. Find the acceleration of each block and tensions in the strings.

View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
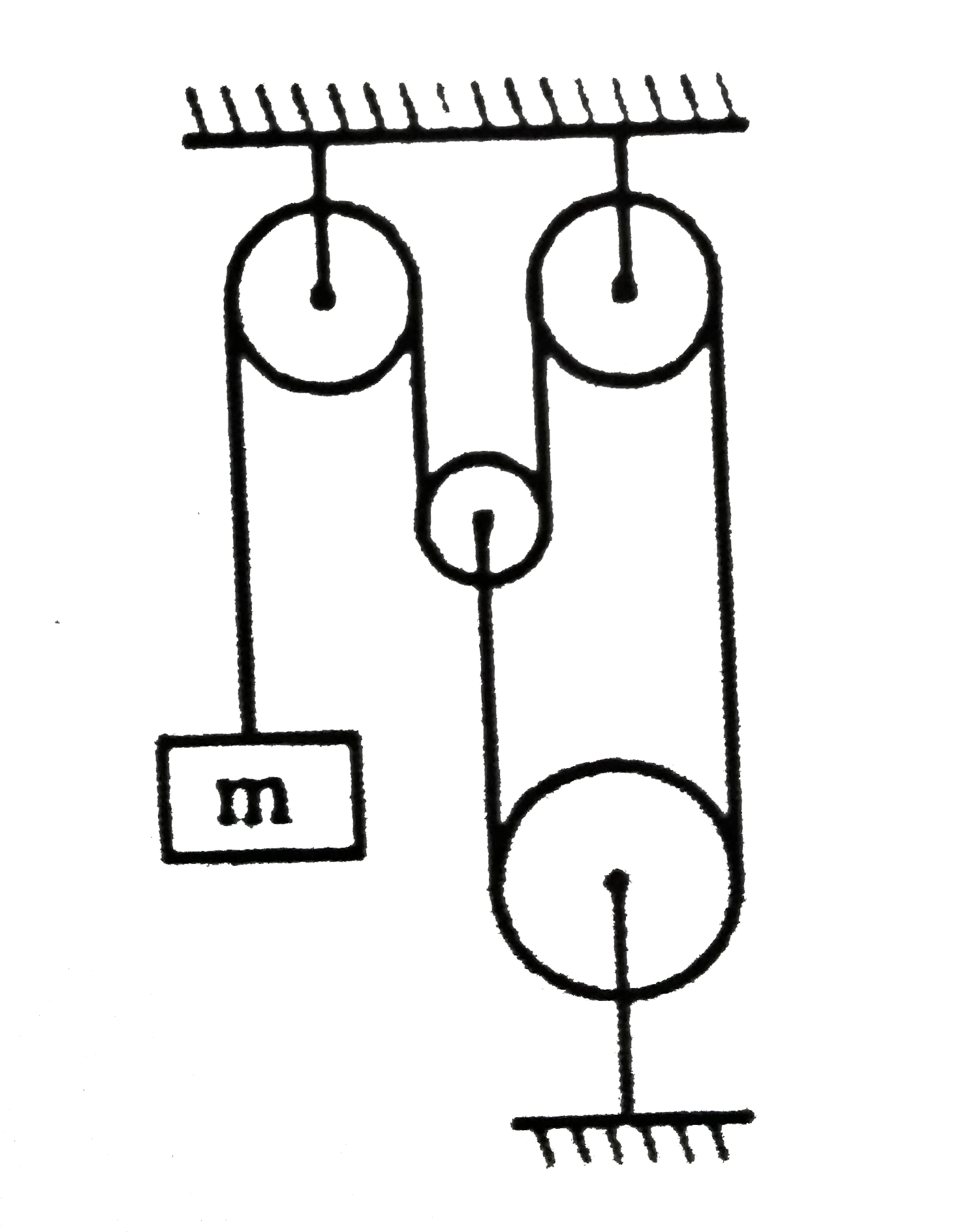
View SolutionIf the string & all the pulleys are ideal, acceleration of mass m is :-
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
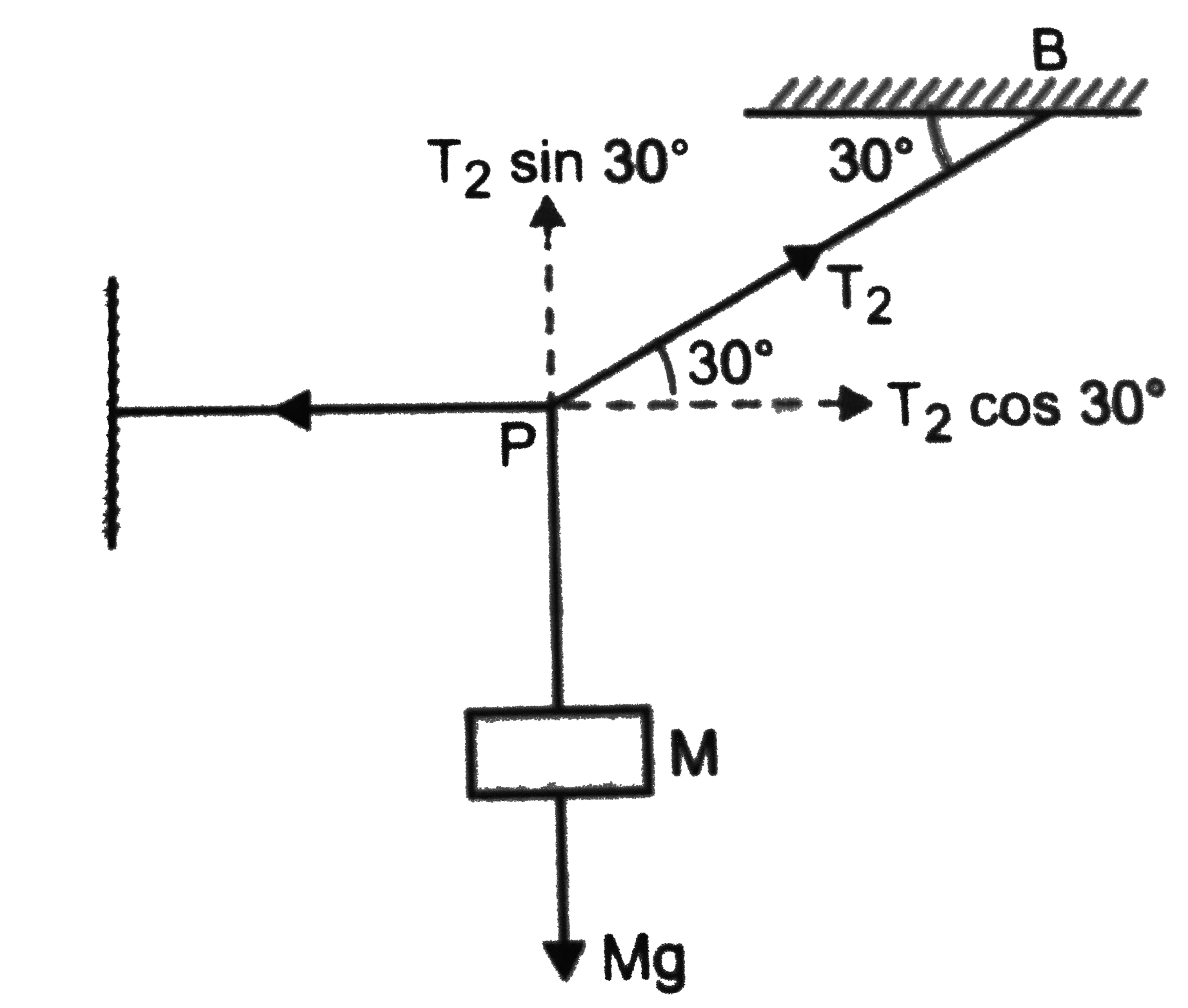
View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
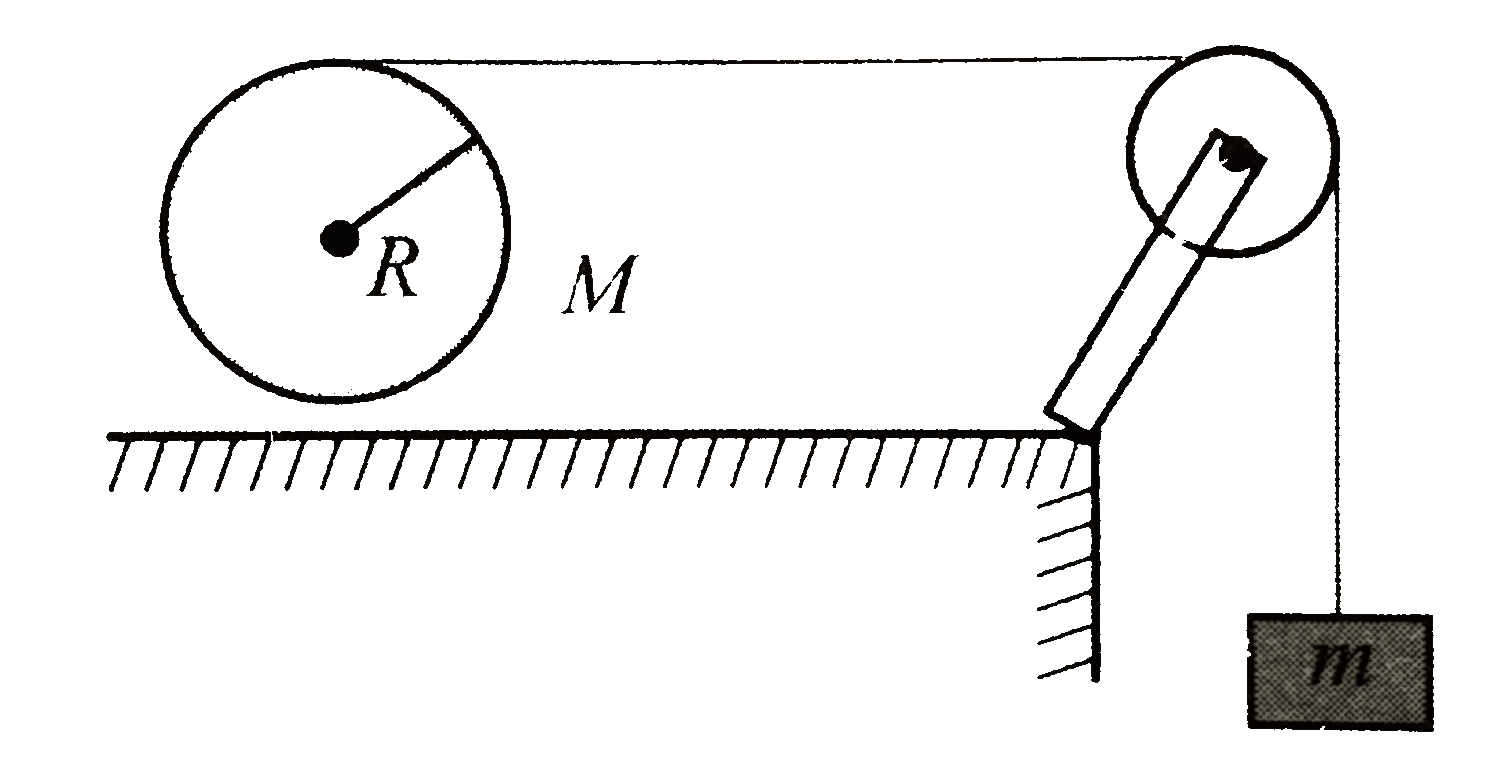
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionA mas m hangs with help of a string wraped around a pulley on a frictionless bearling. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m, if the string does not slip on the pulley, is:
View SolutionWhat is the mechanical advantage of single fixed pulley:-

View Solution
