A tall block of mass $M = 50 k g$ and base width $b = 1 m$ and height $h = 3 m$ is kept on rough inclined surface with coefficient of friction $μ = 0.8$ as shown in figure. The angle of inclination with the horizontal is $37^{\circ}$ . Determine whether the block slides down or topples over.

Video Solution

Text Solution

Verified by Experts

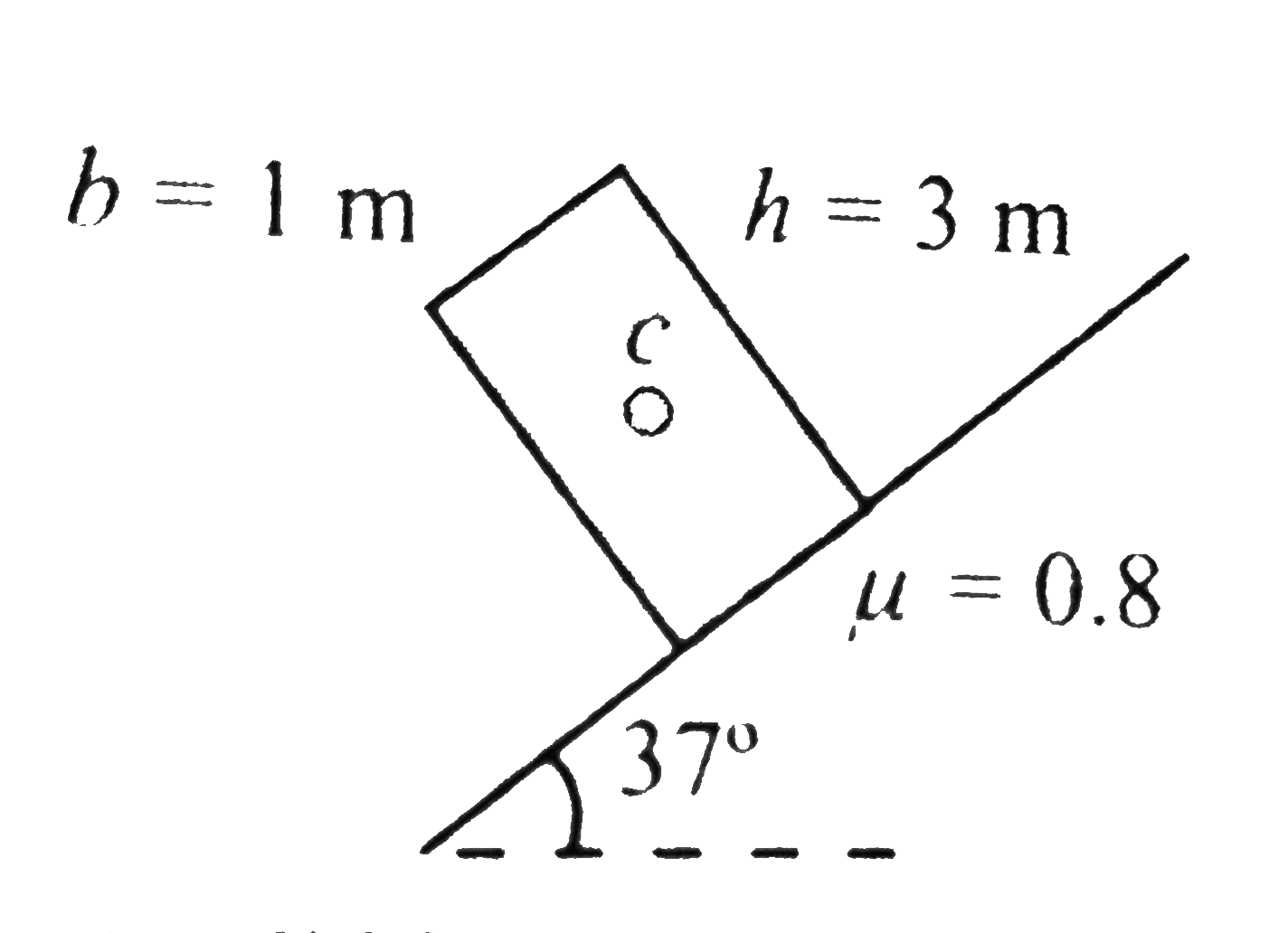
Here $μ = 0.8, \frac{b}{h} = \frac{1}{3}, = 0.33 tan θ = \frac{3}{4} = 0.75$

Since $μ > b / h$ and $μ > tan θ$ , therefore the block has a greater tendency to topple over. From the condition of translation equilibrium , we have
$N = M g {cos 37}^{\circ} = (50) (10) (\frac{4}{5})$ or $N = 400 N$
$f = M g {cos 37}^{\circ} = (50) (10) (\frac{3}{5})$
$= 300 N < f_{mass} = μ N = 0.8 (400) = 320 N$
For rotational equilibrium $Σ τ_{c} = 0$
$N_{x} = f \frac{h}{2}$
Thus, $x = \frac{f}{N} \frac{h}{2} = (\frac{300}{400}) (\frac{3}{2}) = \frac{9}{8} < \frac{b}{2}$
Since the value of $x$ is more than $b / 2$ which is not possible, therefore the block topples over.

Updated on:21/07/2023

A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is Âµ. At what angle of inclination $θ$ of the plane to the horizontal will the block just start to slide down the plane?
A $θ = {tan}^{- 1} μ$
B $θ = {cos}^{- 1} μ$
C $θ = {sin}^{- 1} μ$
D $θ = {sec}^{- 1} μ$
A block of mass m is at rest on an inclined plane. The coefficient of static friction is $μ$ . The maximum angle of incline before the block begins to slide down is :
A ${tan}^{- 1} (μ / m)$
B ${tan}^{- 1} (μ)$
C ${tan}^{- 1} (μ / 2)$
D ${cos}^{- 1} (μ)$
A track has two inclined surface AB and DC each of length 3 m and angle of inclination of $30^{\circ}$ with the horizontal and a central horizontal part of length 4m shown in figure. A block of mass 0.2 kg slides from rest from point A. The inclined surfaces are frictionless. If the coefficient of friction between the block and the horizontal flat surface is 0.2, where will the block finally come to rest ? [in $10^{- 1} m$ ]

A0.5 m away from point B
B3.5 m away from point B
C0.5 m away from point C
D1.5 m away from point C