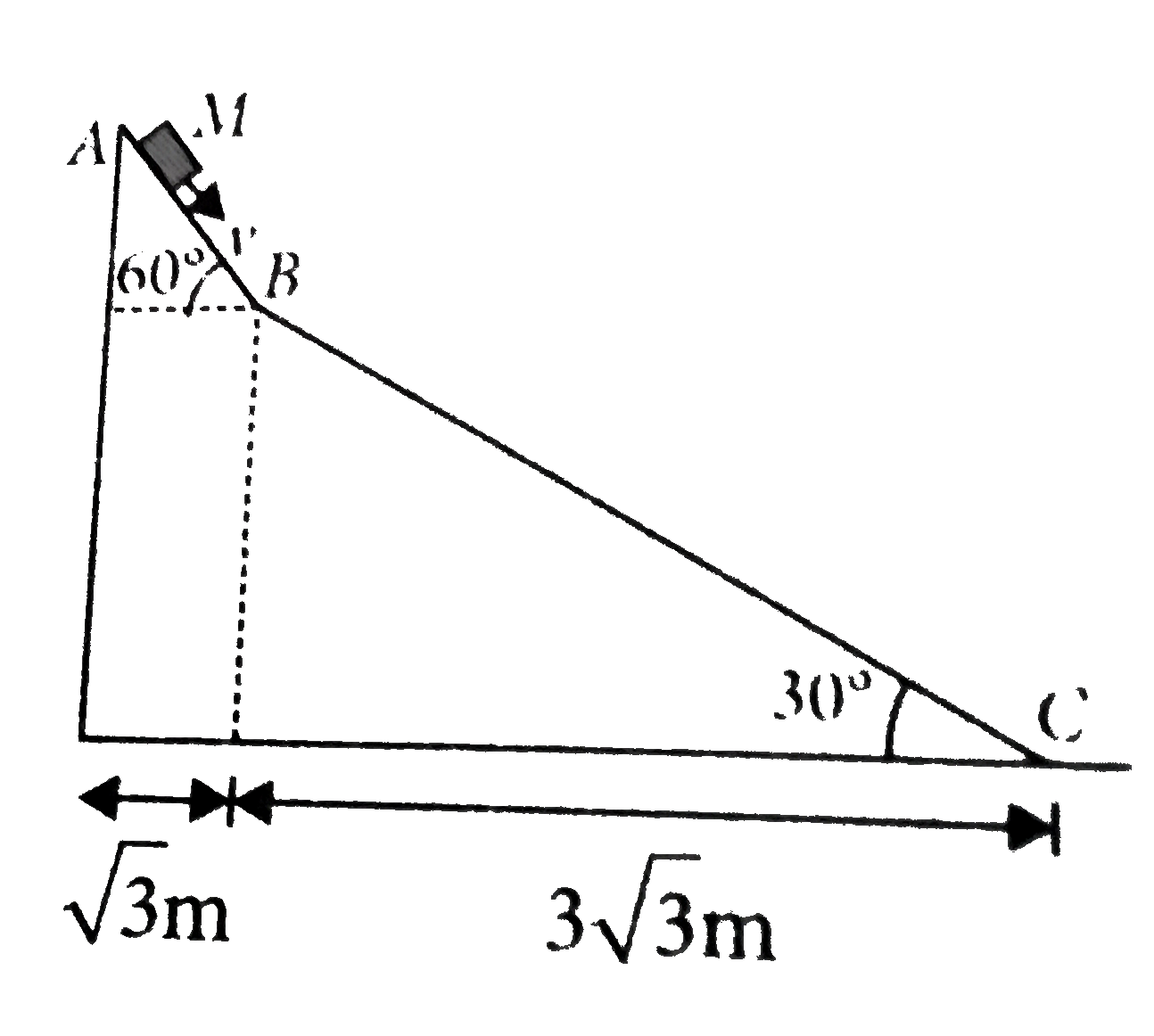
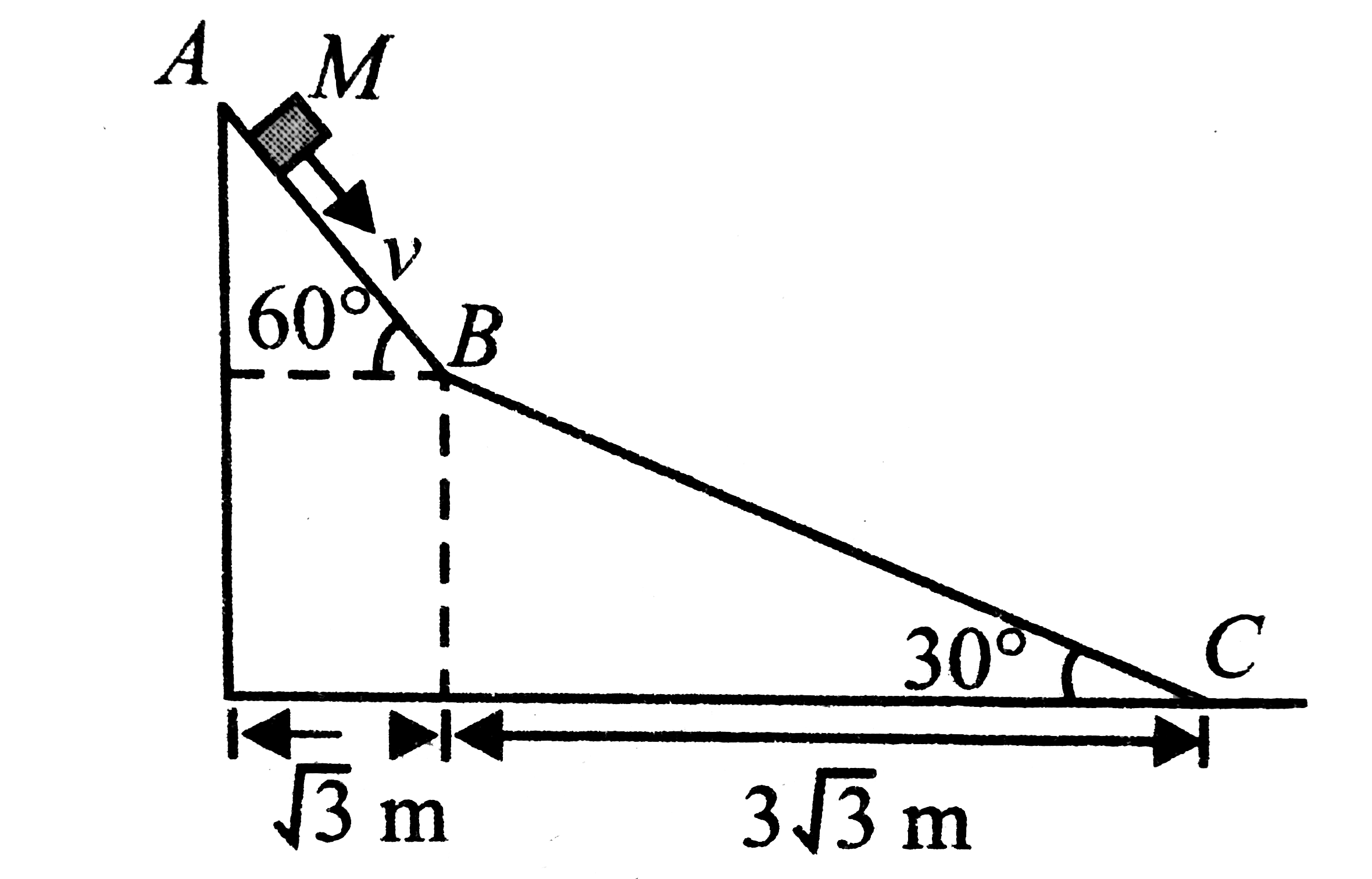
A small block of mass M moves on a frictionless surface of an inclined plane as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is initially at rest at A. Assume that collisions between the block and the incline are totally inelastic. The speed of the block at point B immediately after it strikes the second incline is
√120m/s
√105m/s
√90m/s
√75m/s
The correct Answer is:D
Height fallen by the block from B to C
h2=3√3tan30∘=3m
Let v3 be the speed of the block, at point C just before it leaves the second incline, then
v3=√v22+2gh2=√45+2×10×3=√105m/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - AR_TYPE
1 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
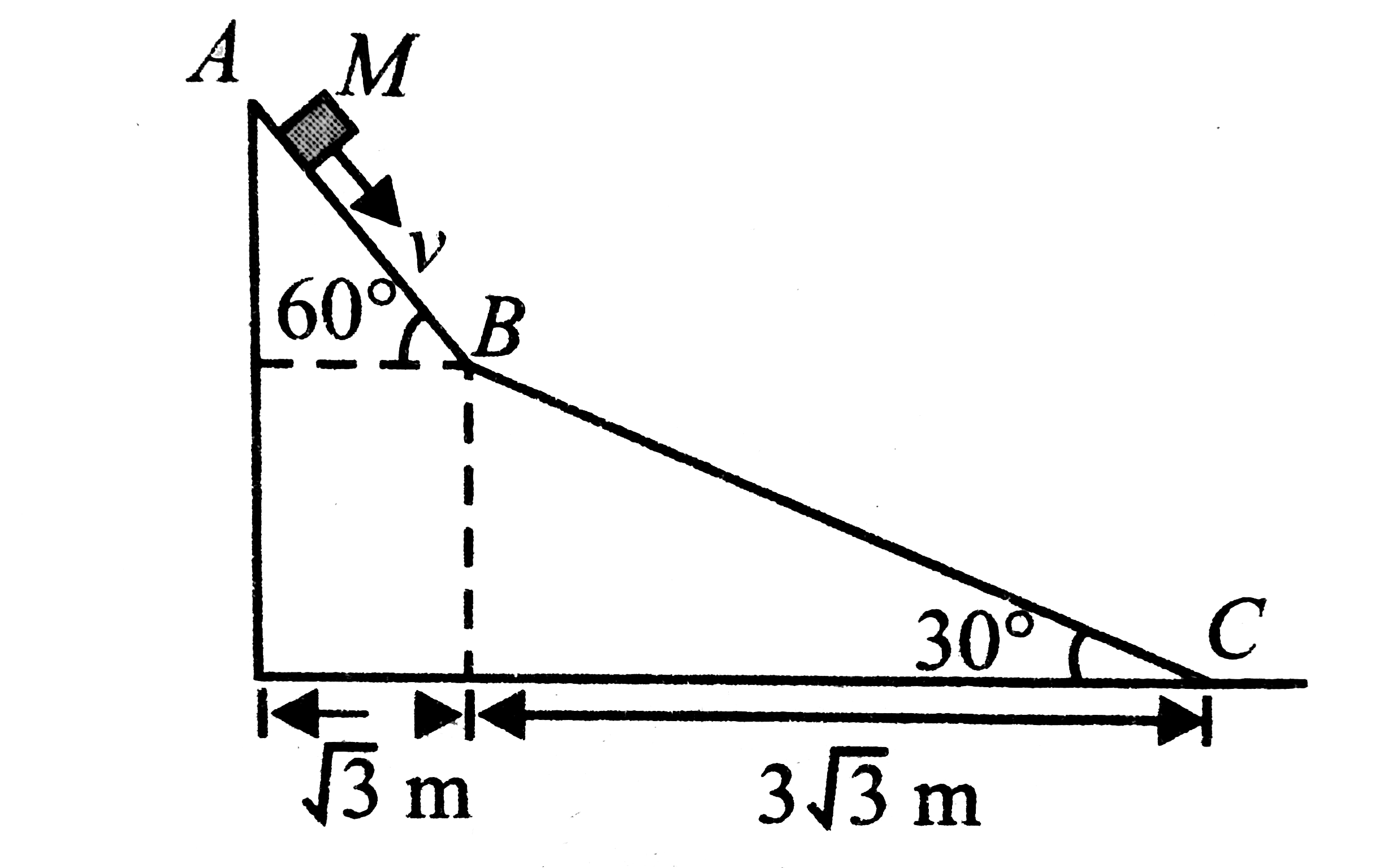
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
View SolutionA small block of mass M move on a frictionless surface of an inclimed from as down is figure . The engle of the inclime suddenly change from 60∘ to 30∘ at point B . The block is initally at rest at A Assume the collsion between the block and the incline are totally inclassic (g=10m/s2)
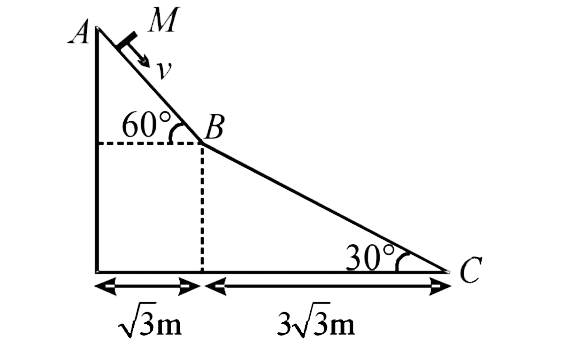
If collision between the block and the incline is completely elestic , then the vartical (apward) component of the of the block at point B immediatly after it stricess the scond indine is -
View Solution
Knowledge Check
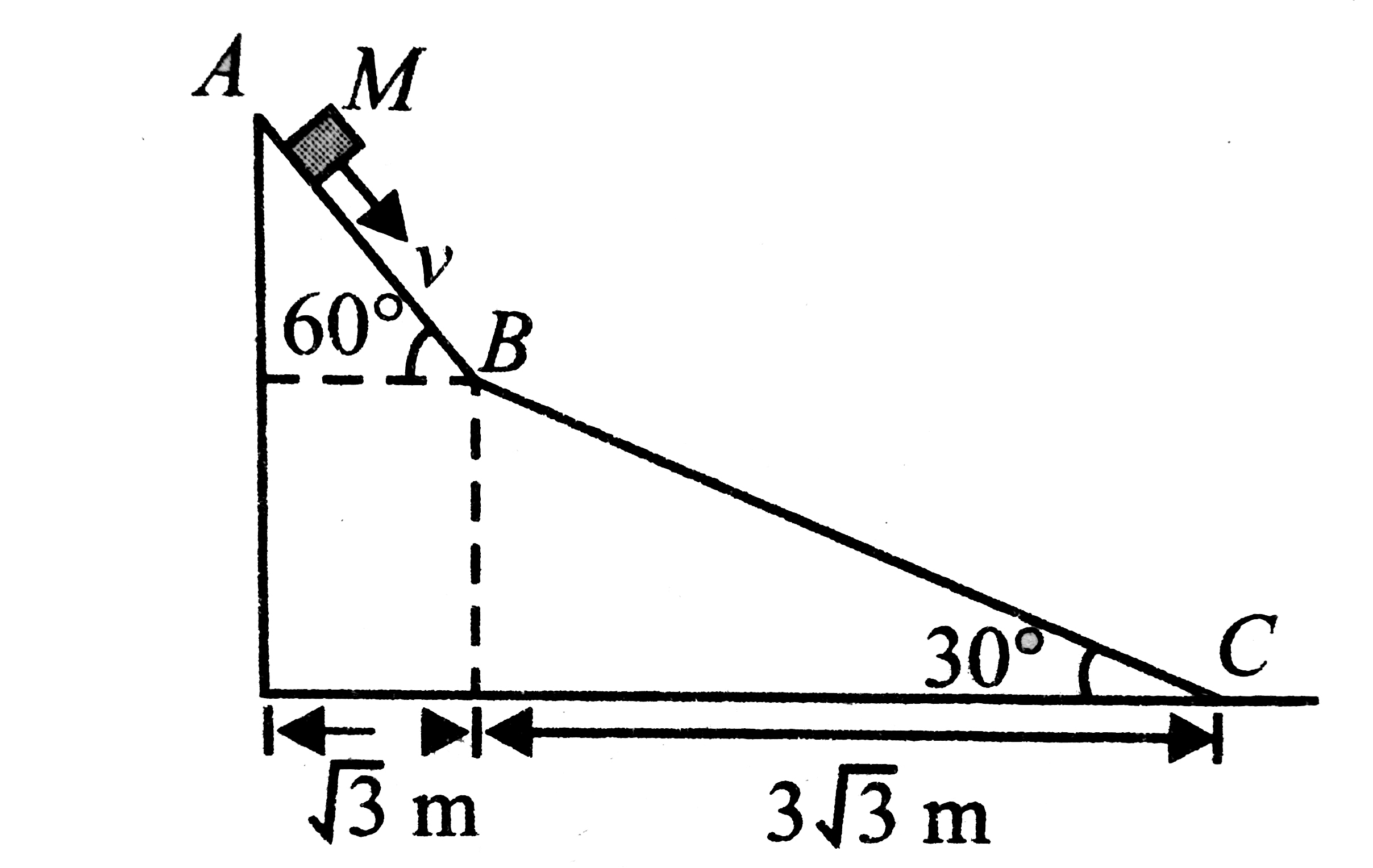
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point B immediately after it strikes the second incline is
 A√60 m/sB√45 m/sC√30 m/sD√15 m/s
A√60 m/sB√45 m/sC√30 m/sD√15 m/sthe speed of the block at point C, immediately before it leaves the second incline is
A√120 m/sB√105 m/sC√90 m/sD√75 m/sA small block of mass M moves on a friction-less surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is initially at rest at A.
If collision between the block and the incline is completely elastic, then the vertical (upward) component of the velocity of the blocks at point B, immediately after it strikes the second incline is
 A√30 m/sB√15 m/sC0D−√15 m/s
A√30 m/sB√15 m/sC0D−√15 m/s
A block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
View SolutionA block of mass 3kg is at rest on a rough inclined plan as shown in the Figure. The magnitude of net force exerted by the surface on the block will be

View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View SolutionTwo blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:

View Solution
