A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
The average elastic force acting on the ball is [m(u+v)]/△t
The average elastic force acting on the ball is [2m(u+v)]/△t
The kinetic energy of the ball increases by 2mu(u+v).
The kinetic energy of the ball remains the same after the collision.
The correct Answer is:B, C
To solve the problem, we need to analyze the elastic collision between a ball and a massive wall. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a ball moving with velocity v towards a massive wall that is moving towards the ball with velocity a. We need to find the average elastic force acting on the ball during the collision and the change in kinetic energy.
Step 2: Determine the Relative Velocity Before Collision
The relative velocity of the ball with respect to the wall before the collision is given by:
vrelative=v+a
This is because both the ball and the wall are moving towards each other.
Step 3: Determine the Velocity After Collision
For an elastic collision, the relative velocity after the collision is equal in magnitude and opposite in direction to the relative velocity before the collision. Thus, we can write:
vrelative after=−(v+a)
Let x be the velocity of the ball after the collision. Then:
x−a=−(v+a)
Solving for x:
x−a=−v−a⟹x=v+2a
Step 4: Calculate Change in Momentum
The momentum of the ball before the collision is:
pbefore=mv
The momentum of the ball after the collision is:
pafter=m(v+2a)
The change in momentum (Δp) is:
Δp=pafter−pbefore=m(v+2a)−mv=2ma
Step 5: Calculate the Average Force
The average force (F) acting on the ball during the collision can be calculated using the formula:
F=ΔpΔt
Substituting the values we found:
F=2maΔt
Step 6: Calculate Kinetic Energy Before and After Collision
The initial kinetic energy (KEinitial) of the ball is:
KEinitial=12mv2
The final kinetic energy (KEfinal) after the collision is:
KEfinal=12m(v+2a)2
Expanding this:
KEfinal=12m(v2+4av+4a2)
Step 7: Calculate Change in Kinetic Energy
The change in kinetic energy (ΔKE) is:
ΔKE=KEfinal−KEinitial=12m(v2+4av+4a2)−12mv2
Simplifying this:
ΔKE=12m(4av+4a2)=2m(a(v+a))
Conclusion
- The average elastic force acting on the ball is:
F=2maΔt
- The change in kinetic energy is:
ΔKE=2m(a(v+a))
We have a ball moving with velocity v towards a massive wall that is moving towards the ball with velocity a. We need to find the average elastic force acting on the ball during the collision and the change in kinetic energy.
The relative velocity of the ball with respect to the wall before the collision is given by:
vrelative=v+a
This is because both the ball and the wall are moving towards each other.
For an elastic collision, the relative velocity after the collision is equal in magnitude and opposite in direction to the relative velocity before the collision. Thus, we can write:
vrelative after=−(v+a)
Let x be the velocity of the ball after the collision. Then:
x−a=−(v+a)
Solving for x:
x−a=−v−a⟹x=v+2a
The momentum of the ball before the collision is:
pbefore=mv
The momentum of the ball after the collision is:
pafter=m(v+2a)
The change in momentum (Δp) is:
Δp=pafter−pbefore=m(v+2a)−mv=2ma
The average force (F) acting on the ball during the collision can be calculated using the formula:
F=ΔpΔt
Substituting the values we found:
F=2maΔt
The initial kinetic energy (KEinitial) of the ball is:
KEinitial=12mv2
The final kinetic energy (KEfinal) after the collision is:
KEfinal=12m(v+2a)2
Expanding this:
KEfinal=12m(v2+4av+4a2)
The change in kinetic energy (ΔKE) is:
ΔKE=KEfinal−KEinitial=12m(v2+4av+4a2)−12mv2
Simplifying this:
ΔKE=12m(4av+4a2)=2m(a(v+a))
- The average elastic force acting on the ball is:
F=2maΔt
- The change in kinetic energy is:
ΔKE=2m(a(v+a))
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
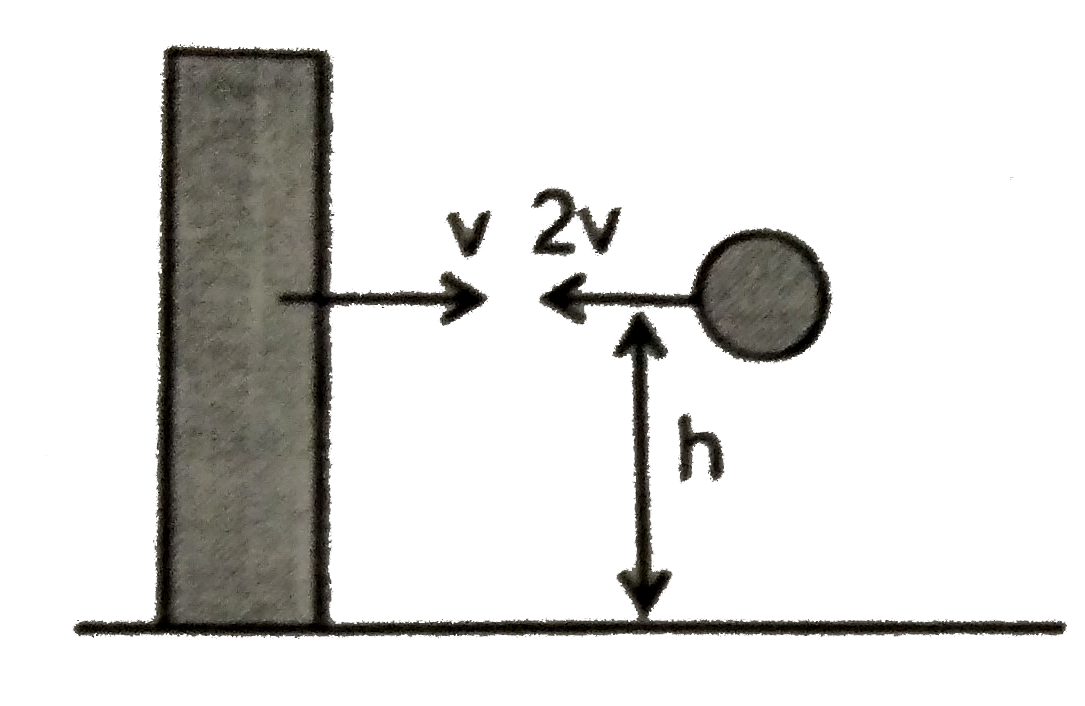
View SolutionA car is moving with velocity →vc towards north and a train is moving towards east with velocity →vt . Find the direction of relative velocity of car with respect to train.
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
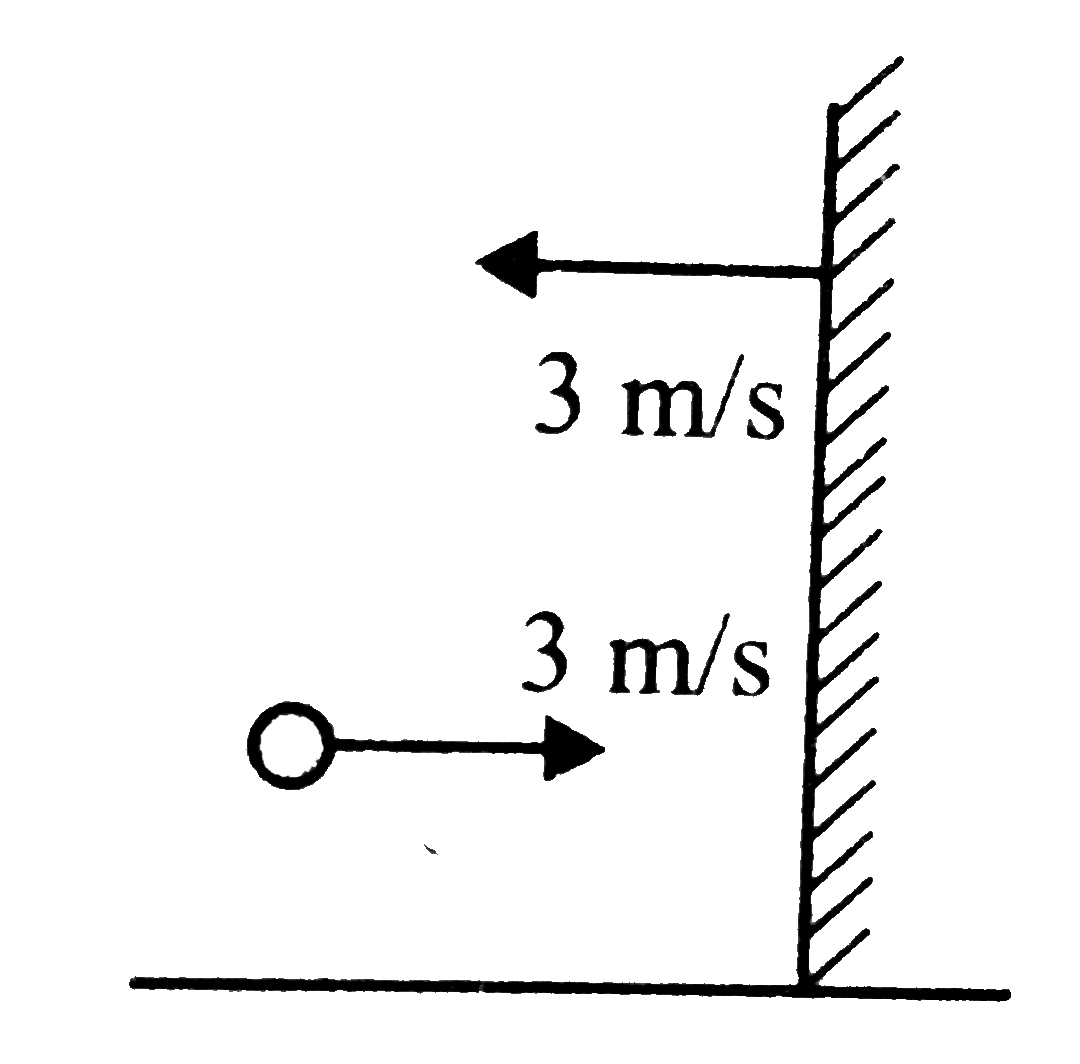
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
View SolutionA cricket ball of mass 150 kg is moving with a velocity of 12m/s and is hit by a bat so that ball is turned back with a velocity of 20m/s . The force of the blow acts for 0.01 s on the ball . Find the average force exerted by the bat on the ball.
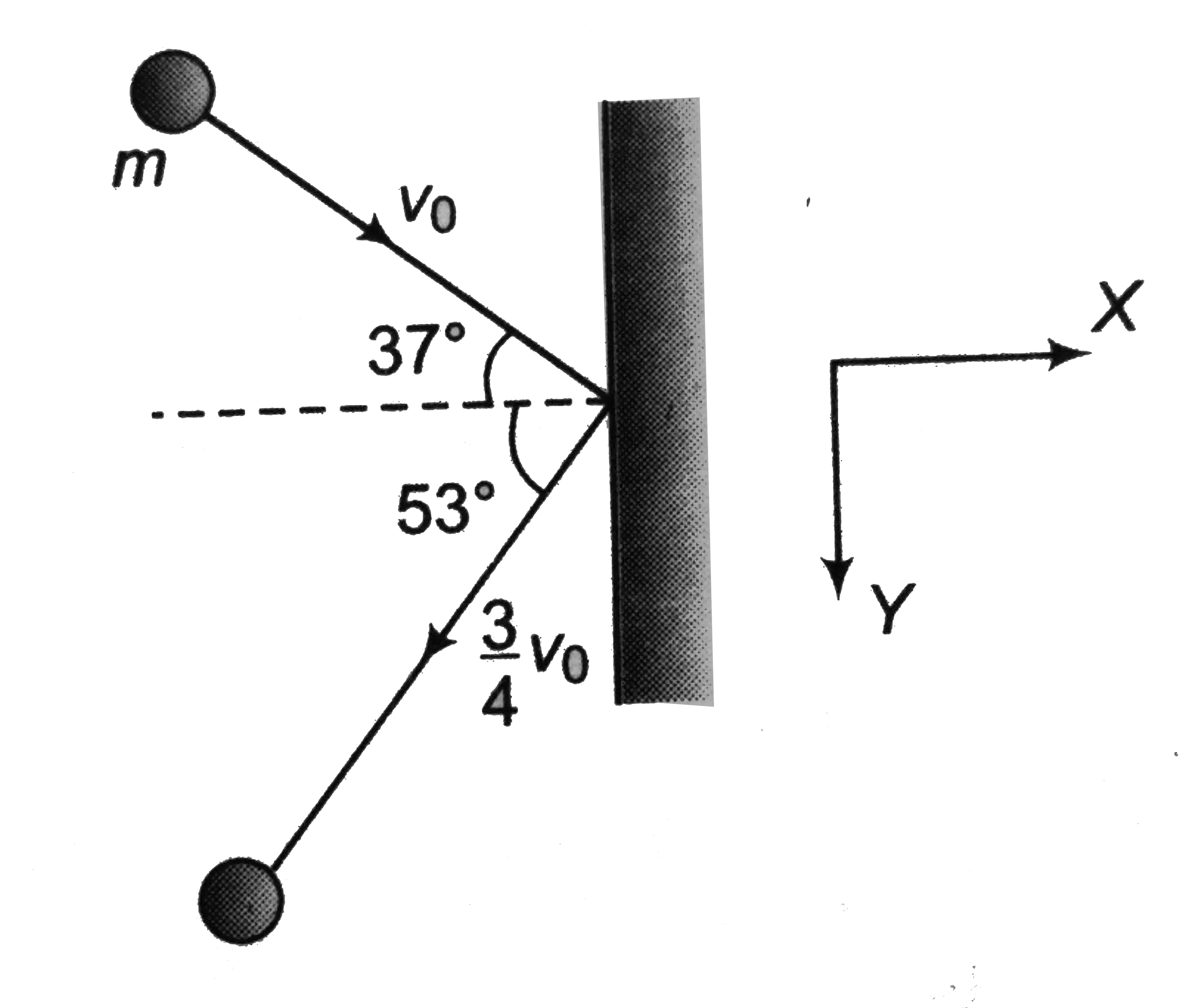
View SolutionA ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is
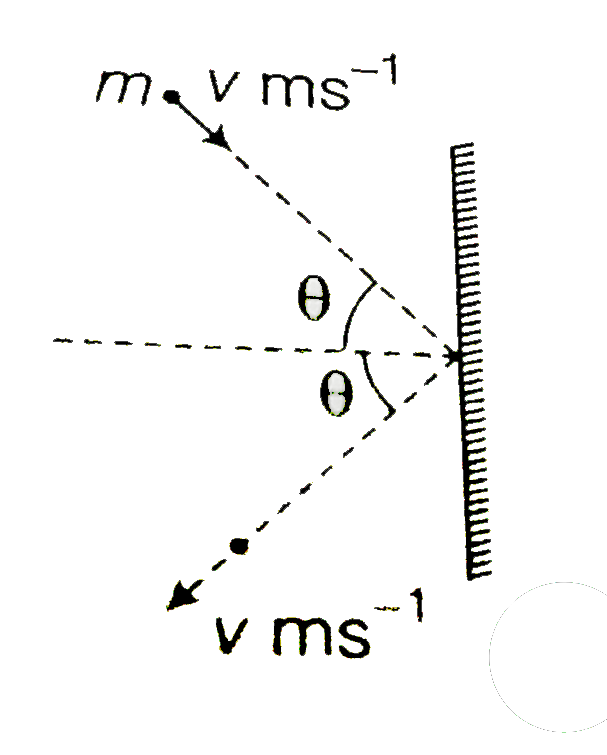
View SolutionA ball is moving towards the wall as shown in diagram then momentum is conserved
View SolutionFind the work done by the wall in reflecting the particle if the particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u. Assuming elastic impact between the particle and wall
View Solution
