In figure, find the velocity of m1 in ms−1 when m2 falls by 9m.
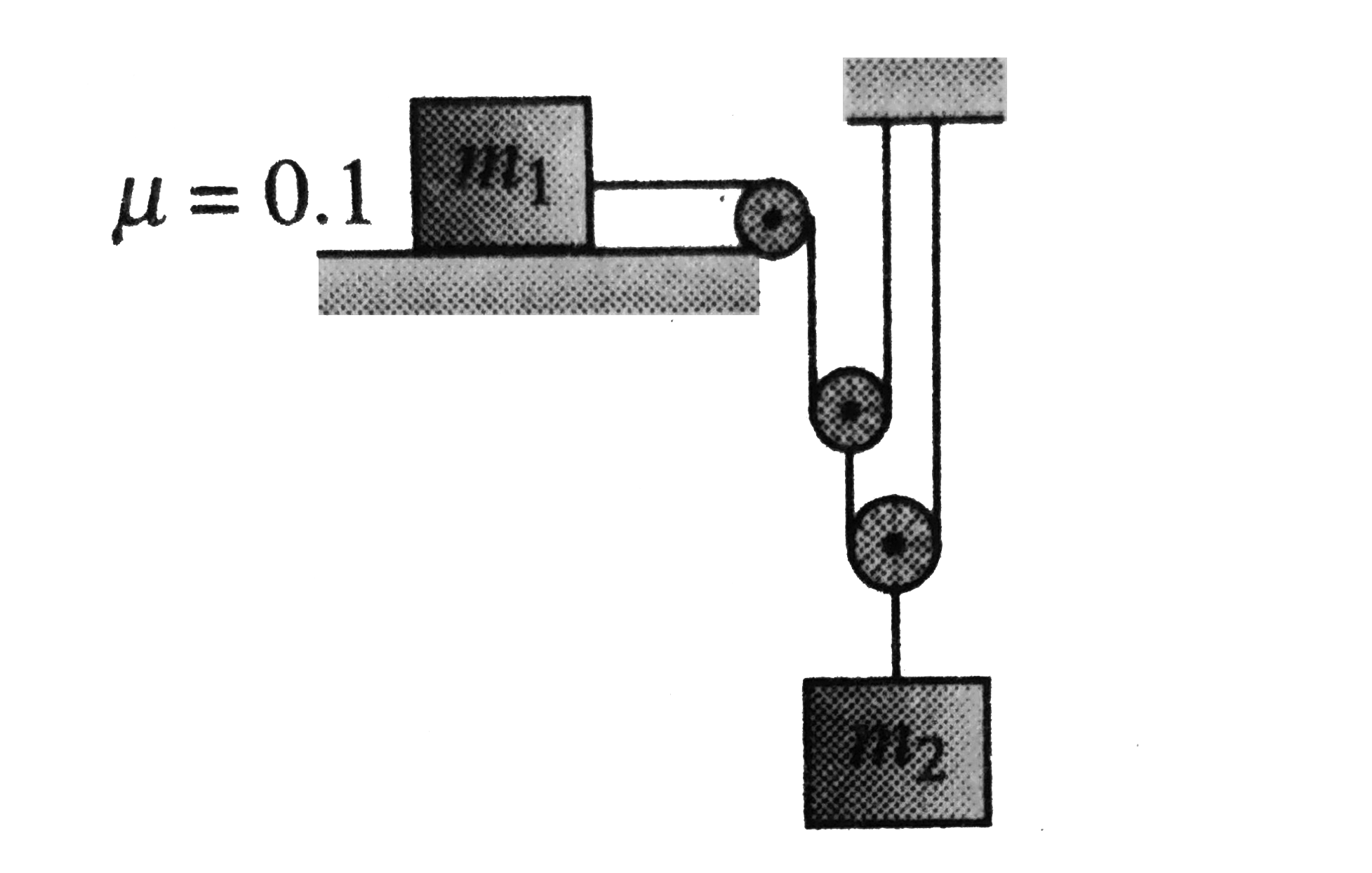
Given m1=m, m2=2m (take g=10ms−2).
The correct Answer is:(4)
From constrains we can show that if at any time velocity of m2 is v, then velocity of m1 will be 4v. Similarly, for displacement.
Applying work-energy theorem, Kf−Ki=Work done =W
12m2v2+12m1(4v)2=m2g×y−μm1g(4y),
where y=9m
⇒v=4ms−1

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
m2−m+1=0 find the value of m
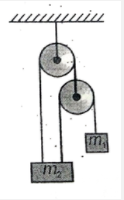
View SolutionIn a given figure the acceleration of M is (g=10ms−2)

View SolutionA person, standing on the roof of a 40 m high tower, throws a ball vertically upwards with speed 10 m/s. Two seconds later, he throws another ball again in vertical direction (use g=10ms2). Both the balls hit the ground simultaneously.
View SolutionIn the given diagram , find the relation between acceleration of blocks m1andm2 . (m2 remains horizontal ).
View SolutionAn object of mass 10 kg falls from rest through a vertical distance of 10 m and acquires a velocity of 10ms−1. The work done by the push of air on the object is (g=10ms−2)
View SolutionA ball rolled on ice with a velocity of 14 ms−1 comes to rest after travelling 40 m . Find the coefficient of friction . (Given g=9.8m/s2
View SolutionA ball rolled on ice with a velocity of 14ms−1 comes to rest after travelling 20 m. Find the coefficient of friction. (Given g=9.8m/s2)
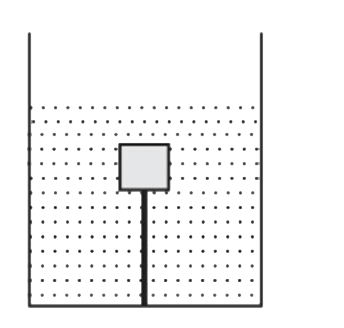
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View Solution
