A spring is compressed between two toy carts to masses m1 and m2. When the toy carts are released, the spring exerts on each toy cart equal and opposite forces for the same small time t. If the coefficients of friction μ between the ground and the toy carts are equal, then the magnitude of displacements of the toy carts are in the ratio
(a) S1S2=m2m1
(b) S1S2=m1m2
(c) S1S2=(m2m1)2
(d) S1S2=(m1m2)2
The correct Answer is:C
Minimum stopping distance=s
Work done against the friction=W=μmgs
Initial momentum gained by both toy carts will be same because same force acts for same time.
Initial kinetic energy of the toy cart =(p22m)
Therefore, μmgs=p22m or s=(p22μgm2)
For the two toy carts, momentum is numerically the same.
Further μ and g are the same for the toy carts.
So, s1s2=(m2m1)2
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Two block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
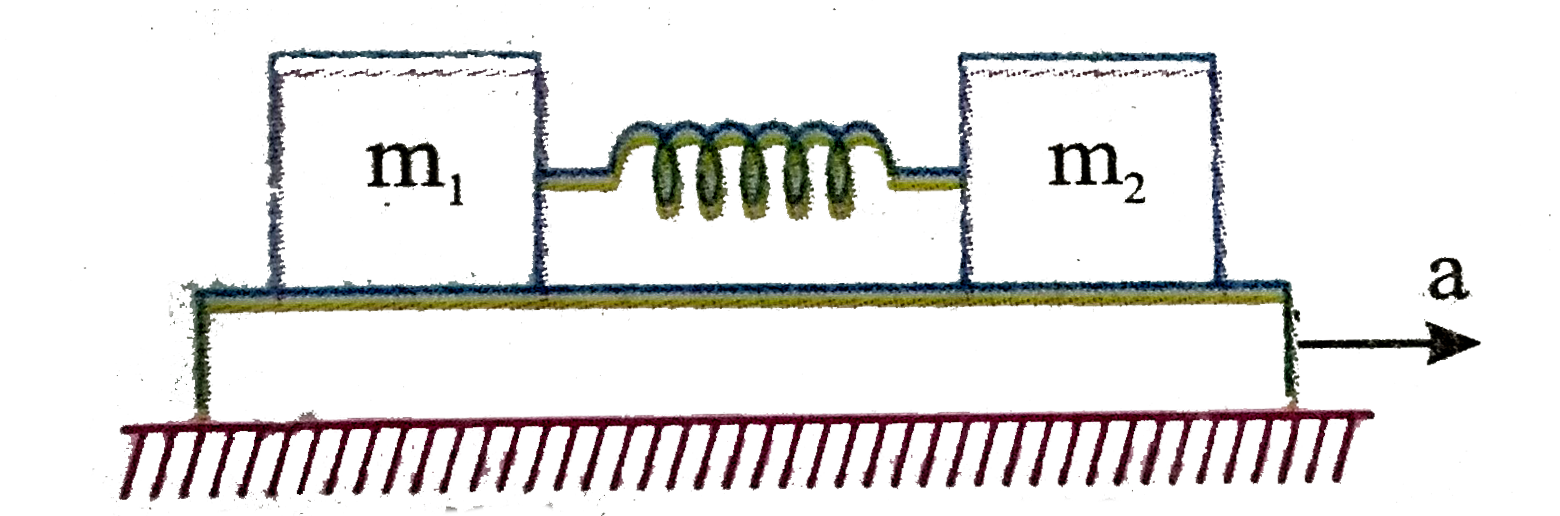 View Solution
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?
 View Solution
View SolutionA block of mass m is in contact with the cart C as shown in The coefficient of static friction between the block and the cart is μ The acceleration a of the cart that will prevent the block from falling satisfies
 .View Solution
.View SolutionA spring is kept compressed by a toy cart of mass 150 g.On releasing the cart.It moves with a speed of 0.2 ms−1 .Calculate the potential energy (elastic)of the spring .
View SolutionA block of mass m is in contact with the cart C as shown in figure -
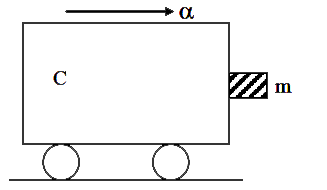
The coefficient of static friction between the block and the cart is μ , The accelertion α of the cart that will prevent the block from failing satisfies -View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View SolutionA cart of mas M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart figure. The string breaks, the bob falls on the floor, makes several collision on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process
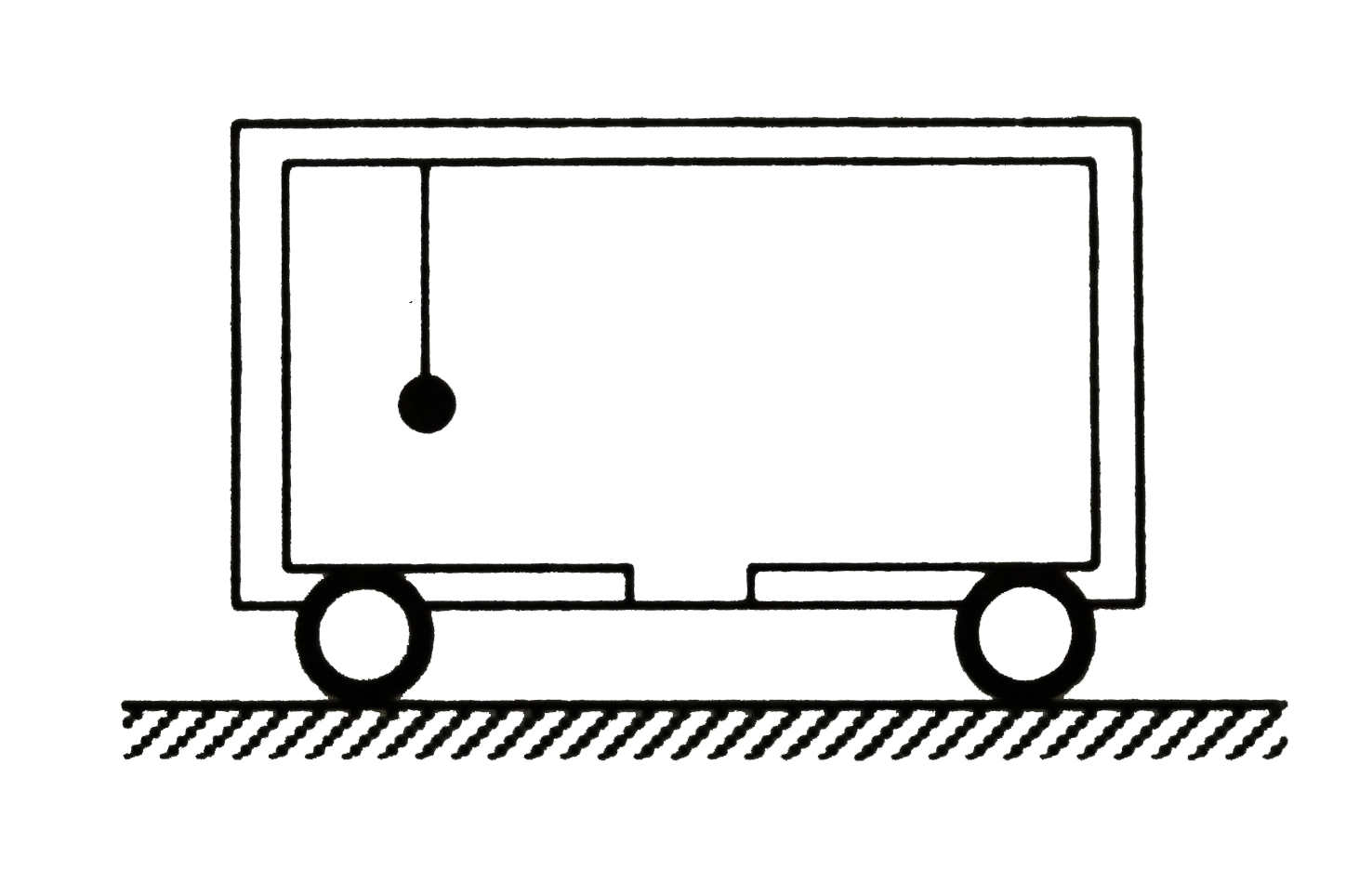 View Solution
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionThe two blocks A and B of equal mass are initially in contact when released from rest on the inclined plane. The coefficients of friction between the inclined plane and A and B are μ1 and μ2 respectiely. Friction is not sufficient to prevent slipping.
 View Solution
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horixontal plane. The cofficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View Solution


