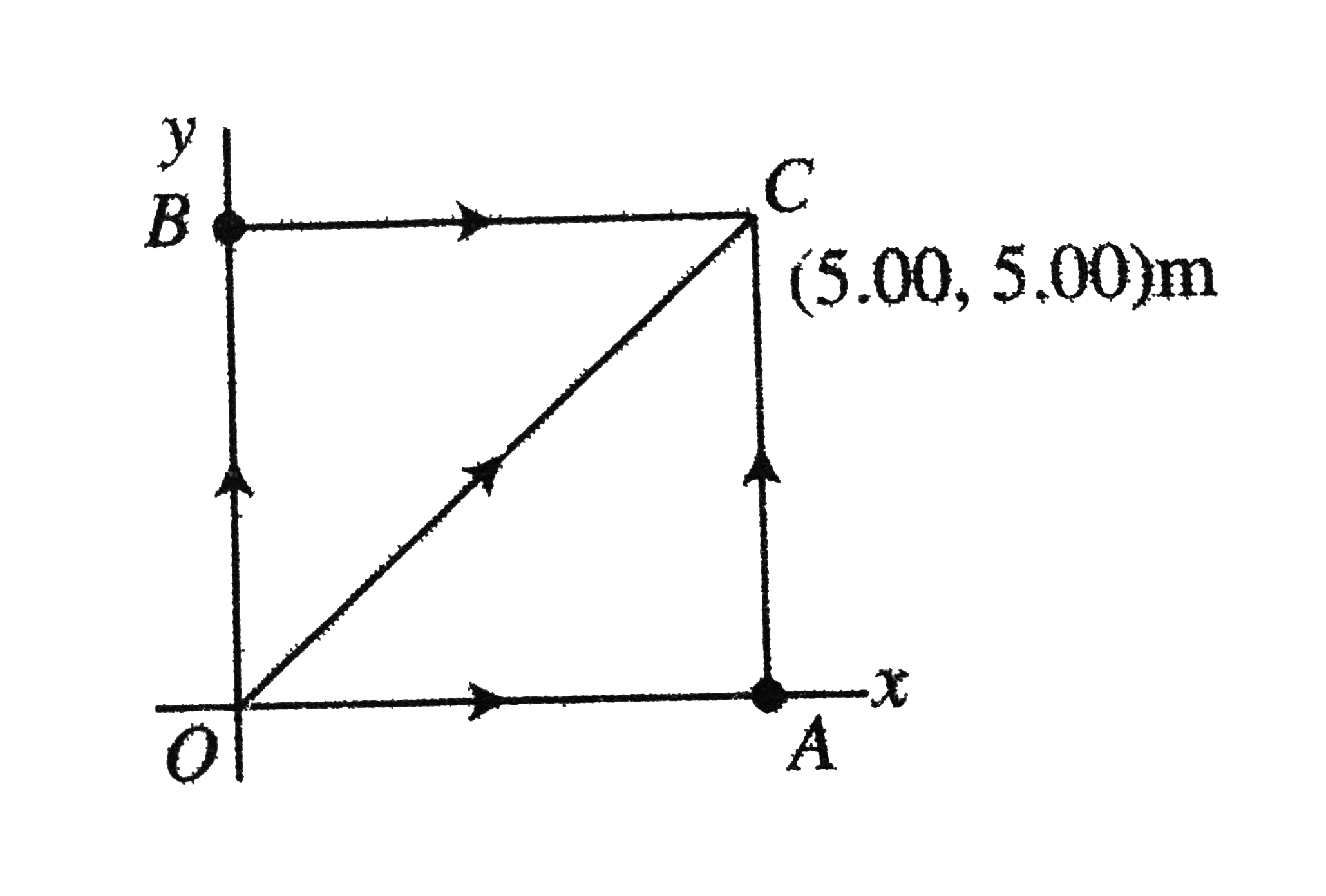
A force acting on a particle moving in the x-y plane is given by →F=(2yˆi+x2ˆj)N, where x and y are in meters. The particle moves from the origin to a final position having coordinates x=5.00m as shown in figure. Calculate the work done by →F on the particle as it moves along (a) OAC, (b) OBC, and (c) OC. (d) Is →F conservative or non-conservative? Explain.
a. For each of the paths from O to C, the work done is given by
W=∫→F⋅→ds
Here →F=(2yˆi+x2ˆj) and →ds=(dxˆi+dyˆj)
Hence W=∫(2yˆi+x2ˆj)(dxˆi+dyˆj)
⇒W=5∫02ydx+5∫0x2dy ...(i)
The path OAC can be break up into two paths, from O to A and then from A to C.
First considering path O to A, in this path y=0, hence from equation (i) it is clear WOA=0
Now consider path A to C, in this path x is constant (i.e., dx=0) and is equal to 5m. From equation (i)
WAC=x25∫0dy=(5)2[y]50=125J
Hence total work done WOAC=0+125=125J
b. Now consider the path OBC, this path also break up into two paths O to B and then B to C.
Considering path O to B, in this path x=0, hence from equation (i) it is clear WOB=0.
Now considering path B to C, in this path y is constant (i.e. dy=0) from equation (i)
WBC=2y5∫0dx=2×5×[x]50=50J
Hence total work done in this path, WOBC=0+50=50J
c. Motion of the particle from O to C, in this path both x and y are charging. In this path x=y⇒dx=dy
From equation (i),
WOC=5∫0(2x+x)2dx=2[x22]50+[x33]50
=25+13×125=2003J
d. We have calculated the work done from O to C in three different paths which is not same, hence the force F is a non-conservative force.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples15videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Force acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
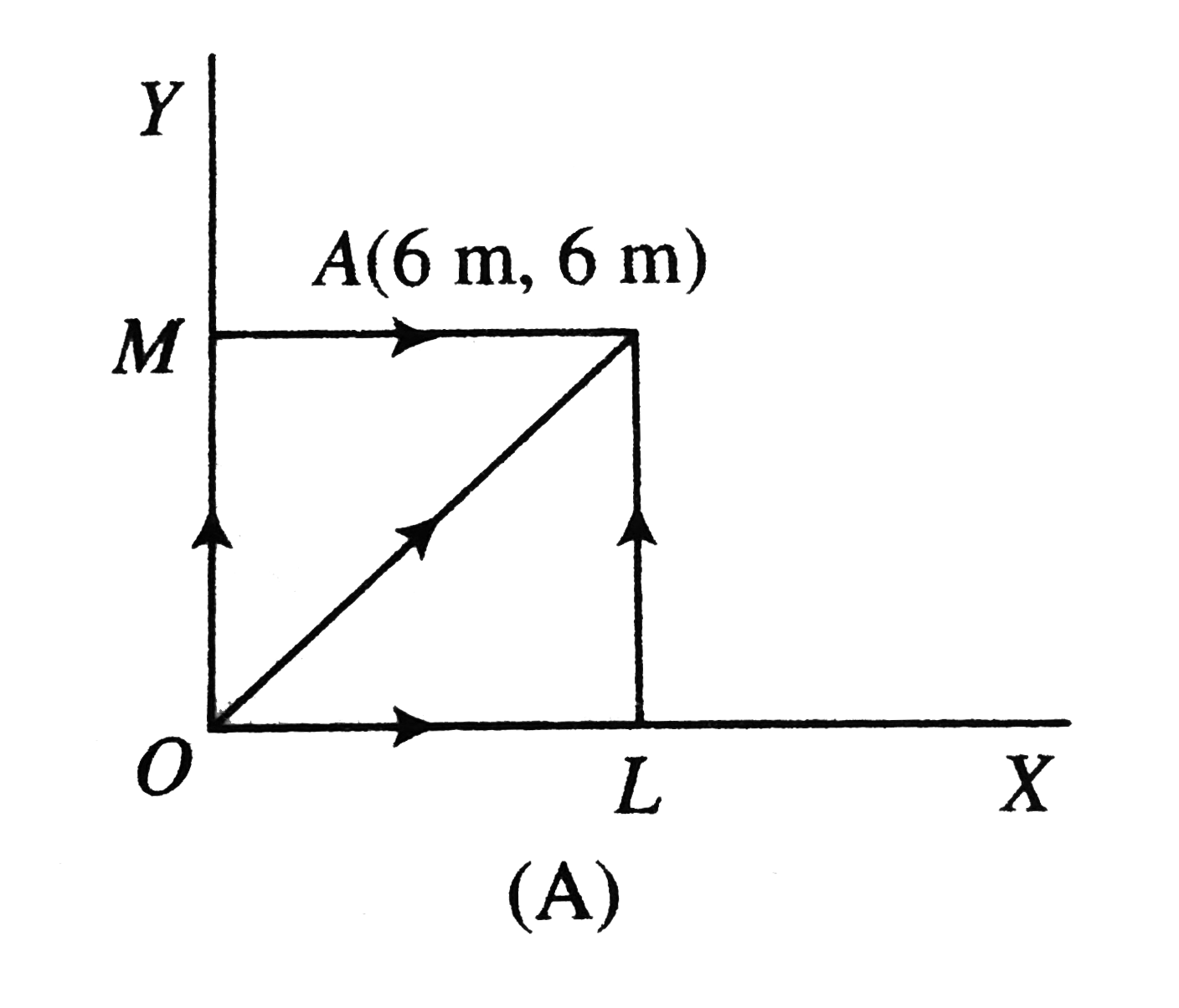
Work done for motion along path OA is nearly
 View Solution
View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.
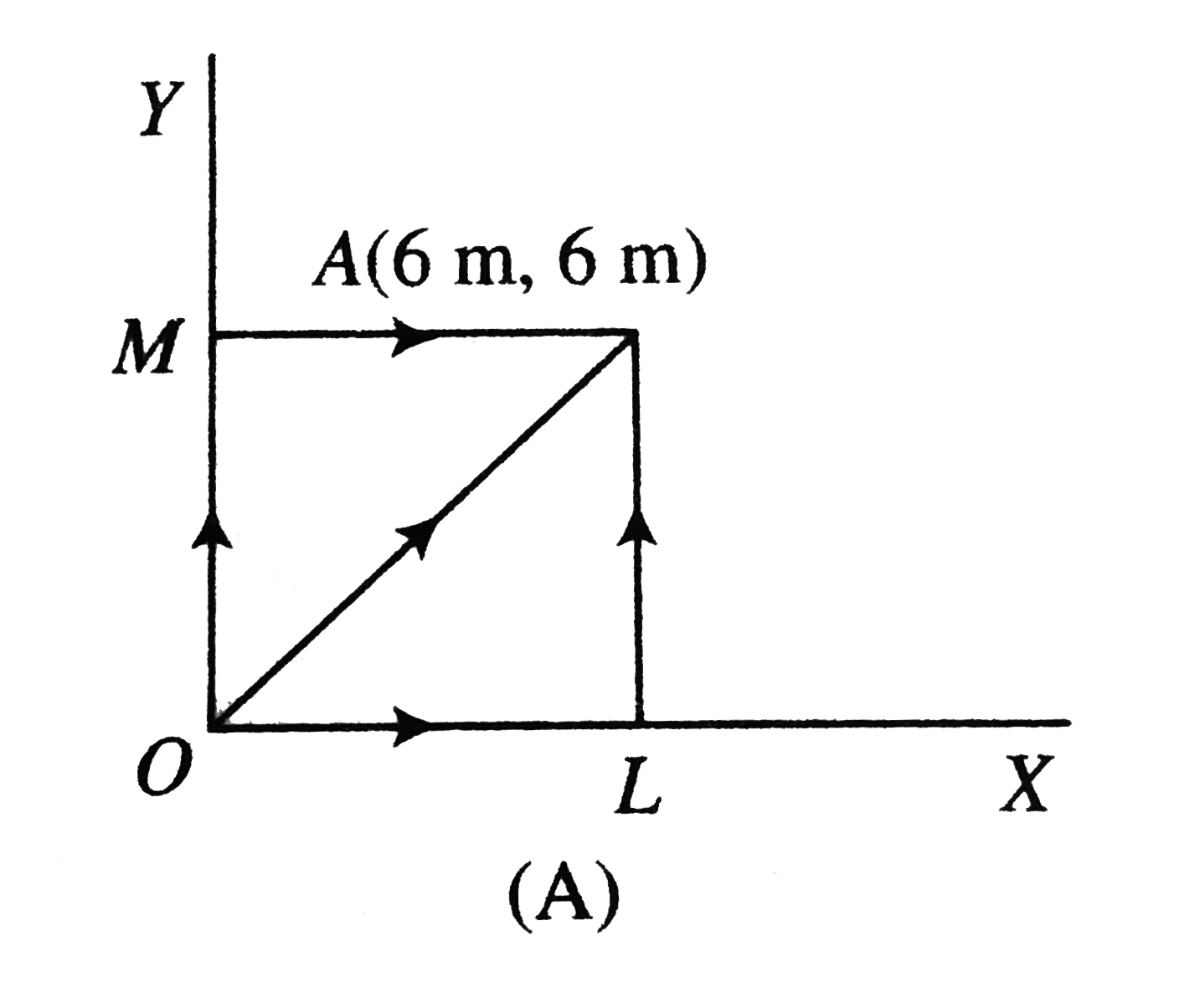
Which of the following is correct?View SolutionForce acting on a particle moving in the x-y plane is →F=(y2ˆi+xˆj)N, x and y are in metre. As shown in figure, the particle moves from the origin O to point A (6m,6m). The figure shows three paths, OLA, OMA, and OA for the motion of the particle from O to A.

Which of the following is correct?View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle of mass 1 kg moving in X-Y plane is given by U=(12x+5y) joules, where x an y are in meters. If the particle is initially at rest at origin, then select incorrect alternative :-
View SolutionA particle moves in the x−y plane , accoding to the equation, r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
 View Solution
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View Solution
