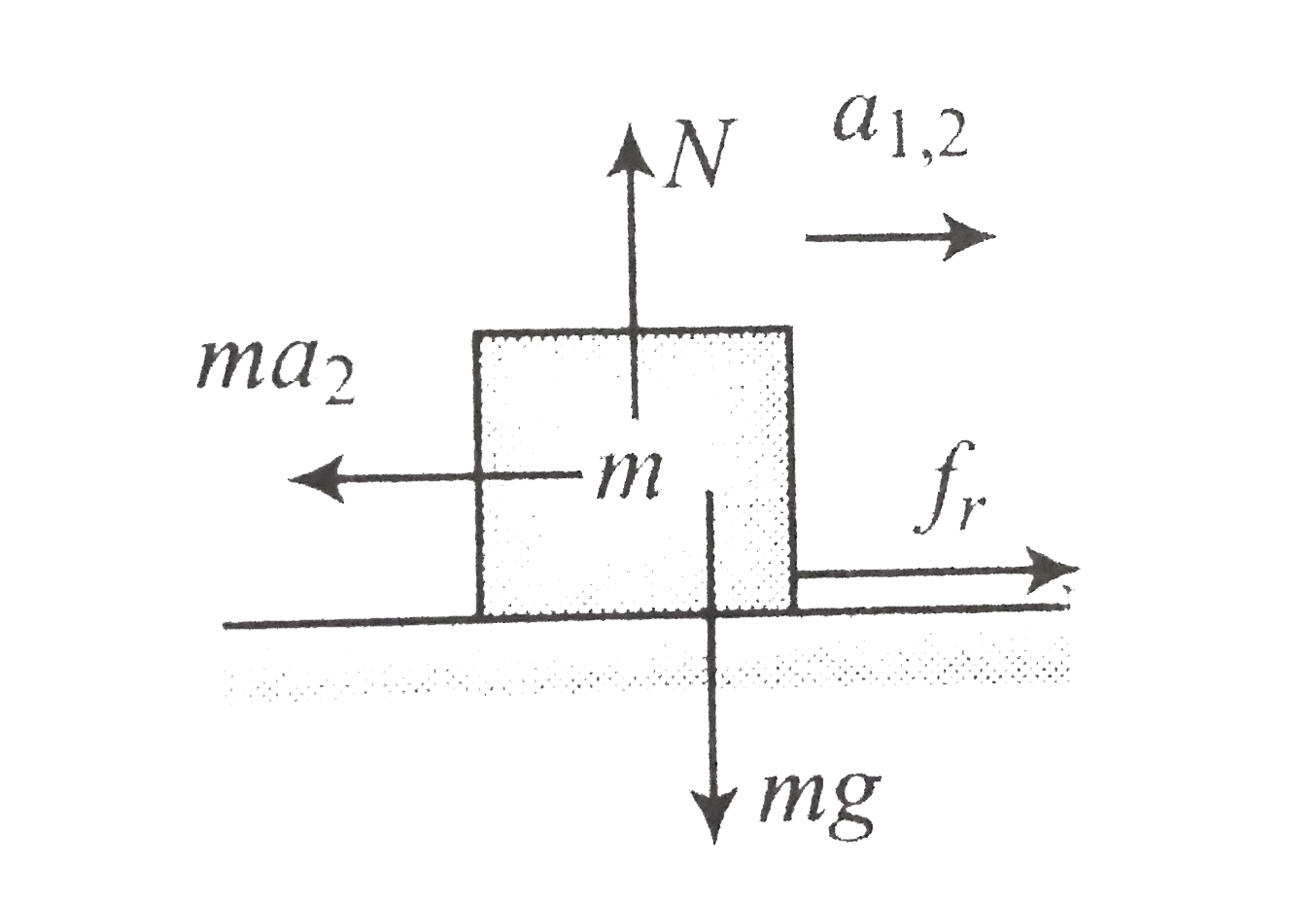
A block of mass m1 moves with an acceleration a12 relative to a trolley as shown in figure. The block is being observed by two observers (2) and (3). The observer (2) is at rest with respect to trolley which is moving with acceleration a2 while the observer(3) is moving on ground with acceleration a3. What is the work done by the pseudo force as observed by the observers (2) and (3) on the block during time t? Assume zero intial velocities of the bodies and observers.

The observer(2) will observer a pseudo force of magnitude ma2 in the direction opposite to the acceleration of observer(2) as shown in figure.
The displacement of the block will respect to trolley (observer2),
d12=12a12t2
Hence, work done by pseudo force on block as shown by observer(2),
W2=−(ma2)⋅(d12)
=−ma212a12t2
=−12ma2⋅a12t2
The observer(3) will observe a pseudo force ma3(←).
For calculating the work done by pseudo force as seen from observer(3) (W3), we need to calculate displacement of the block w.r.t. observer (3) (i.e., s13).
→s13=12→a13t2
a13=→a1−→a3=(→a12+→a2)−→a3=(a12+a2−a3)
⇒s13=12(a12+a2−a3)t2
Hence, W3=−(ma3)s13=−(ma3)[12(a12+a2−a3)t2]
→a=→a13=→a1−→a3=→a12+→a2−→a3=(a12+a2−a3)t2
Using the above equations, we have
Wpseudo=−ma32(a12+a2−a3)t2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
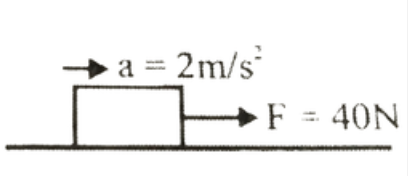
A block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
View Solution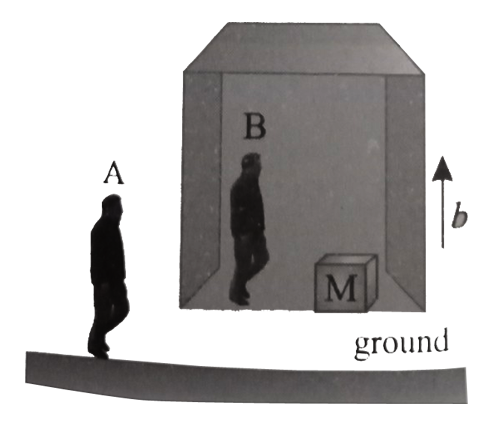
A block of mass M is kept in elevator (lift) which starts moving upward with constant acceleration b as shown in figure. Initially elevator at rest. The block is observed by two observers A and B for a time interval t=0 to t=T. Observer B is at rest with respect to elevator and observer A is standing on the ground.
Q. The observer A finds that the work done by gravity on the block is
View Solution
A block of mass M is kept in elevator (lift) which starts moving upward with constant acceleration b as shown in figure. Initially elevator at rest. The block is observed by two observers A and B for a time interval t=0 to t=T. Observer B is at rest with respect to elevator and observer A is standing on the ground.
Q. The observer A finds that the work done by gravity on the block is
View Solution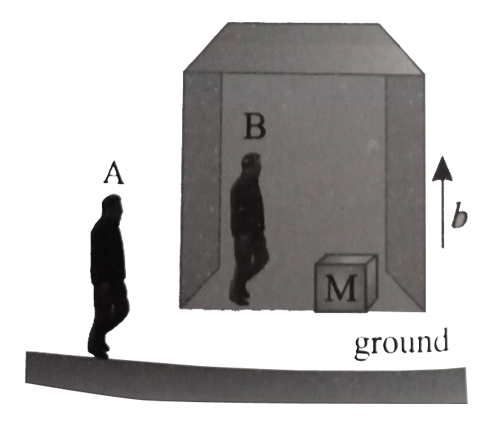
A block of mass M is kept in elevator (lift) which starts moving upward with constant acceleration b as shown in figure. Initially elevator at rest. The block is observed by two observers A and B for a time interval t=0 to t=T. Observer B is at rest with respect to elevator and observer A is standing on the ground.
Q. According to observer B
View SolutionA smooth block of mass m moves up from bottom to top of a wedge which is moving with an acceleration a10. Find the work done by the pseudo force measured by the person sitting at the edge of the wedge.

View SolutionA source of sound moves towards an observer
View SolutionA source of sound moves towards an observe.
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
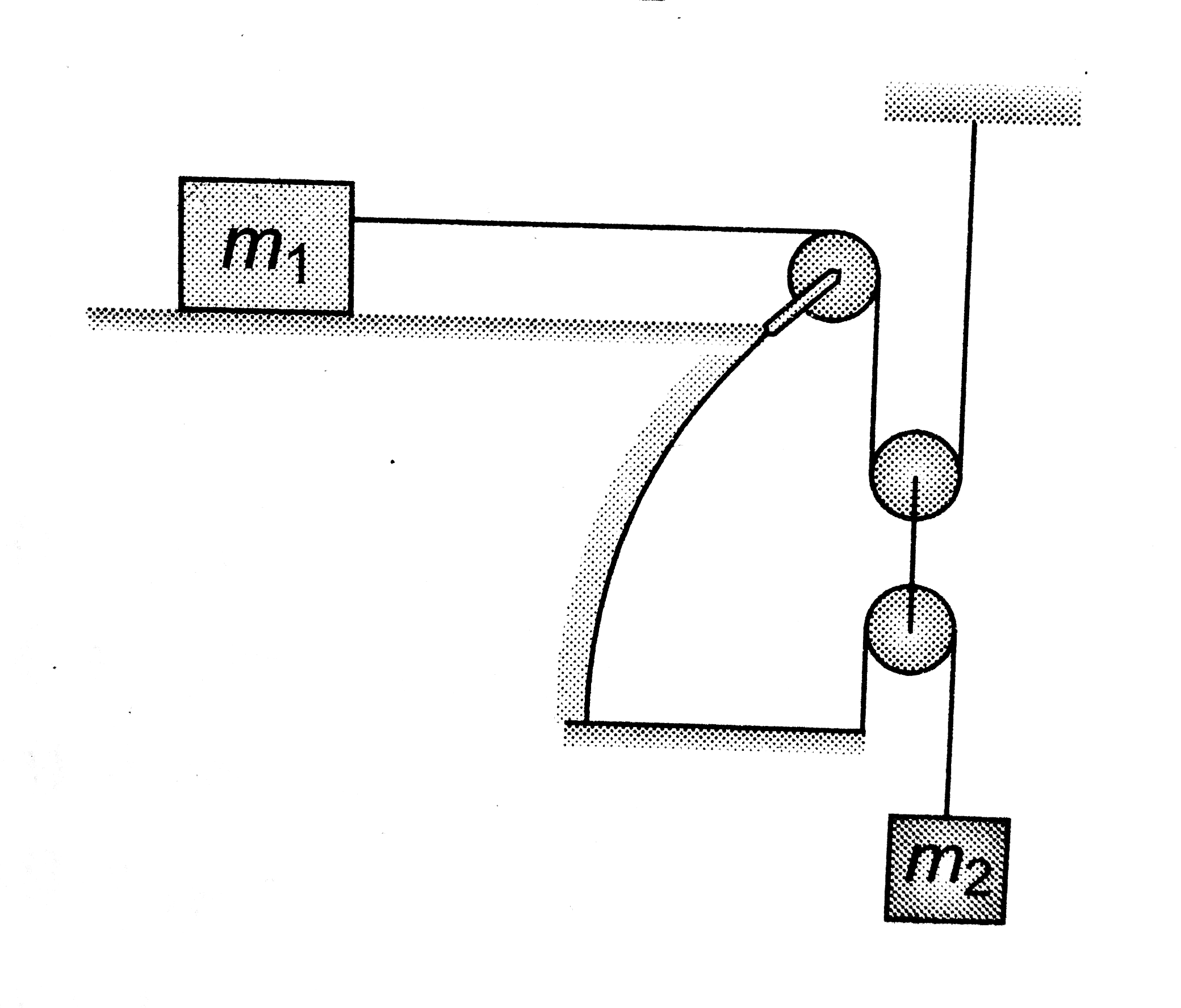
View Solution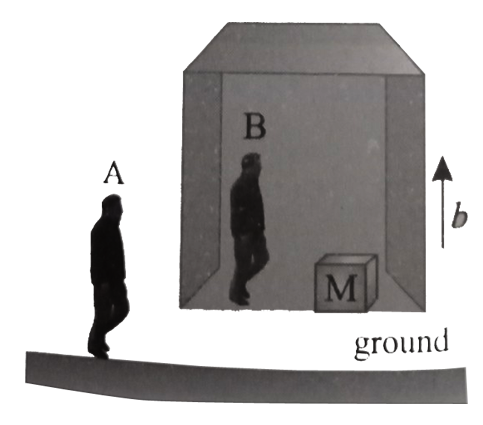
A block of mass M is kept in elevator (lift) which starts moving upward with constant acceleration b as shown in figure. Initially elevator at rest. The block is observed by two observers A and B for a time interval t=0 to t=T. Observer B is at rest with respect to elevator and observer A is standing on the ground.
Q. The observer A finds that work done by normal reaction acting on the blocks is
View Solution
A block of mass M is kept in elevator (lift) which starts moving upward with constant acceleration b as shown in figure. Initially elevator at rest. The block is observed by two observers A and B for a time interval t=0 to t=T. Observer B is at rest with respect to elevator and observer A is standing on the ground.
Q. The observer A finds that work done by normal reaction acting on the blocks is
View Solution
