A particle of m1 moves in a circular path of radius R on a rotating .A string connecting the particles m1 and m2 passes over a smooth hole made on the table as shown in figure If mass m1 does not slide relative to the rotating table , mark the correct option as applicable.
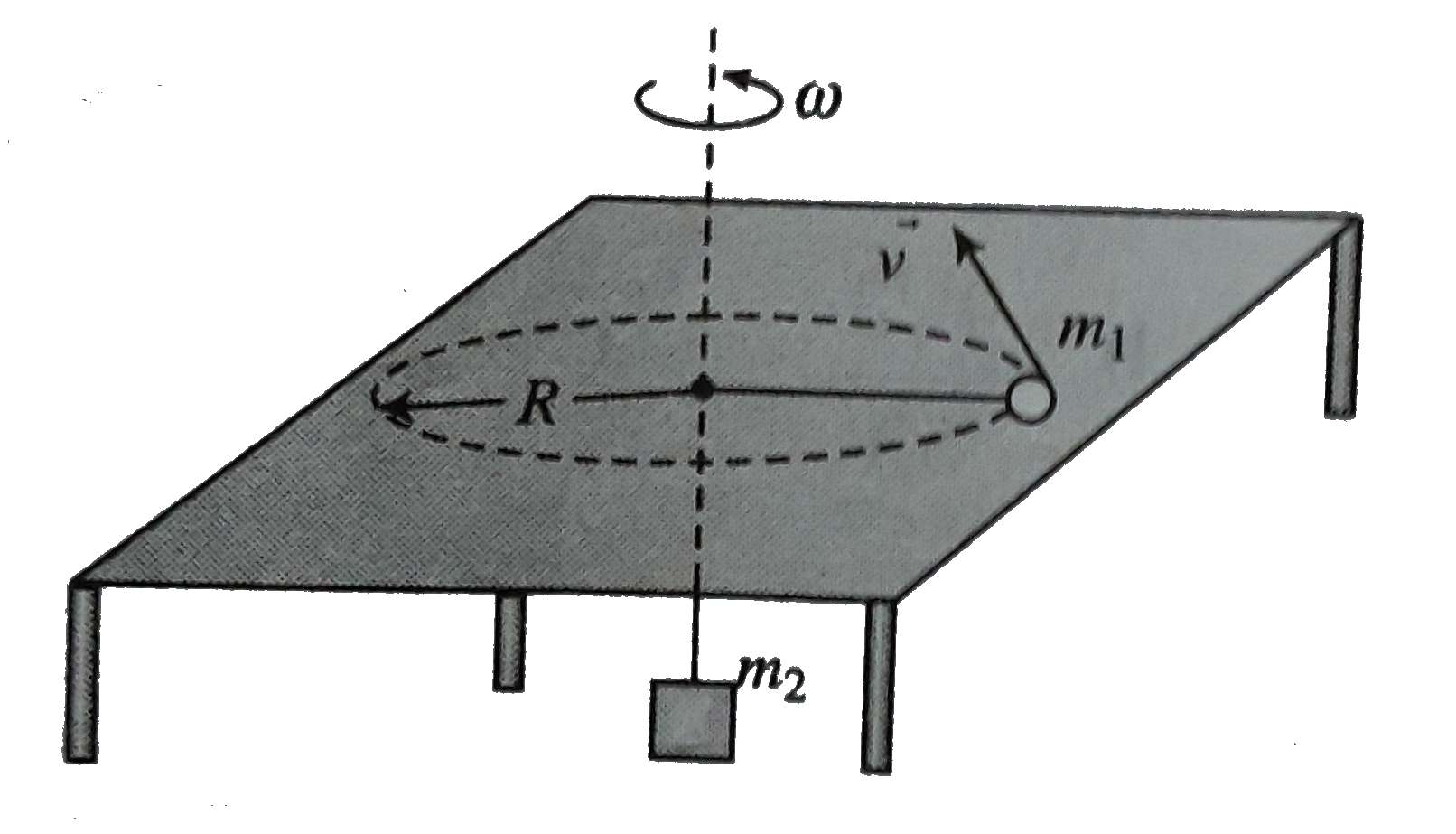
The friction force acting on the block m1is(m1ω2R−m2g) along radial rotation towards center of rotation
The friction force acting on the block m1is(m1ω2R−m2g) along tangential direction in the direction oppesite to→v
The maximum angular velocity of the particle is √(m2+μm1m1)gR
The minimum angular velocity of the particle is √(m2−μm1m1)gR
The correct Answer is:a,c,d
FBD Let the friction radially inward .The force on m1 are f←(assumed),T←N↑mtg↓ The force on m2 are m2g↓andT↑ as shown in figure
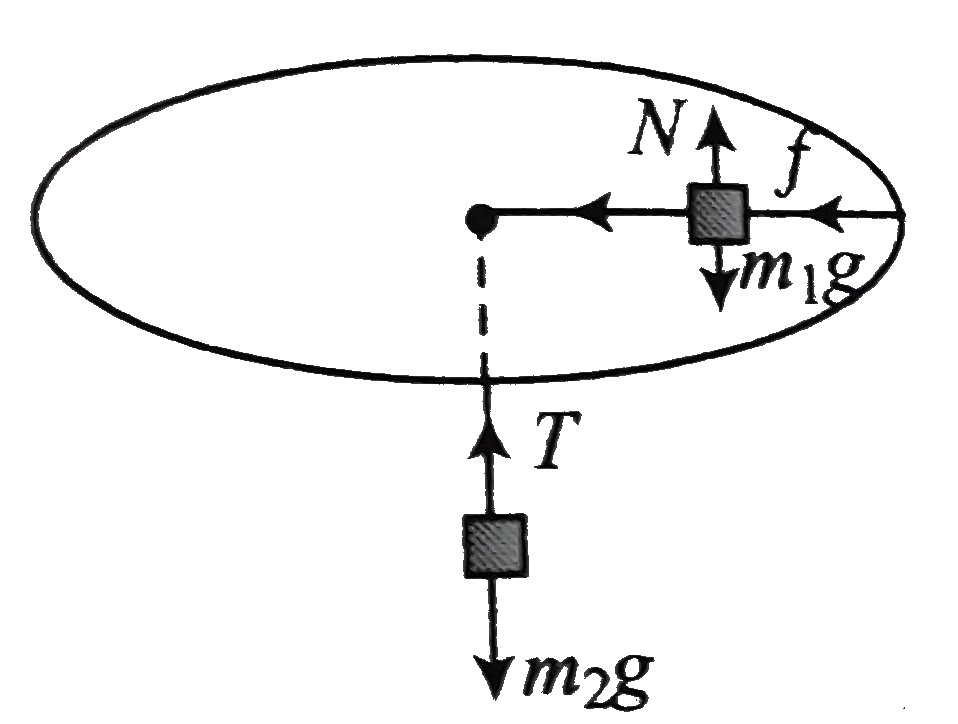 Force equation:
Force equation:
For m1:
∑Fy=N−m1g=maa1y (i)
∑Fr=f+T=m1ar (ii)
Fro m2:
∑Fy=T−m2g=m2a2y (iii)
Law of static friction:
f≤μN
Kinematics: a1y=0
ar=v2R
a2y=0 (vii)
Solving the above equations, we have
f=m1v2R−m2g or m1ω2R−mg
Now substituinh the above value of f and N in Eq (iv).
we have (m1v2R−m2g)≤μm1g
This gives vmax=√(m2+μm1m1)gR
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple Correct
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Linked Comprehension
Explore 52 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Subjective
Explore 21 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View SolutionA Particle of mass 'M' moves in a uniform circular path of radius 'r' with a constant speed 'v' then its centripetal acceleration is .
View SolutionA particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
View SolutionTwo blocks of mass m1andm2 lie on smooth horizontal table in contact with each other as shown in figure
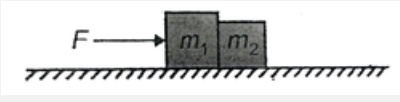
If a force F is applied to the mass m1 then the contact force between the block will be
View SolutionA particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View SolutionA particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is

View SolutionA particle of-mass m moves along a circular path of radius r with velocity v. What is its instantaneous angular momentum about a point on the plane of the orbit at a distance x from the centre of the axis of rotation.
View SolutionThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View Solution

