Consider the setup is of a Ferris wheel in an amusement part. The wheel is turning in acounterclockwise manner Contrary i.e. parralel to the x- axis Determine the orienation of the normal to seat as it passes point A

parallel to the x- axis
in the first/third quadrants
parallel to the y- axis
in the second/fourth quadrants
The correct Answer is:d
F is contrifogal force Net force is along AB so seat will so aligned along AB
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Your are riding on a Ferris wheel that is rotating with a constant speed . The car in which you are riding always maintain its correct upward orientation , it does not invert.
a. What is the direction of the normal force on you form the seat when you are at the top of the wheel ?
i. upward ii. downward .iii. impossible to determine
b. From the same choices, what is the direction of the net force on you when you are at the top of the wheel?
View SolutionA magnetic field is established by a circular current i of radius a. Find the magnetic field gradient (i.e. the derivative of the magnetic field induction vector) in the direction of the circular current's axis at a point whose distance from the centre of the turn is x.
View Solution
Knowledge Check
Consider a uniform electric field E=3×103ˆiN/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a 60∘ angle with the x-axis ?
A10NC−1m2B20NC−1m2C30NC−1m2D40NC−1m2
The general motion of a rigid body can be considered to be a combination of (i) a motion …. of its centre of mass about an axis, and (ii) its motion about an instantaneous axis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless stick, as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω , the motion at any instant can be taken as a combination of (i) a rotation of the centre of mass of the disc about the z-axis, and (ii) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case.

Now consider two similar systems as shown in the figure: case (a) the disc with its face vertical and parallel to x-z plane, case (b) the disc with its face making an angle of 45° with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the system are rotated with constant angular speed ω about the z-axis
Which of the following statement regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct ?
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
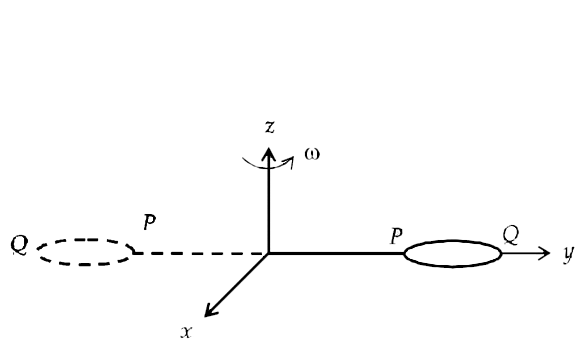
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
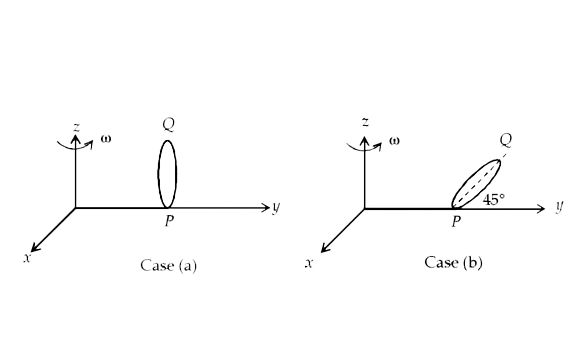
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View Solution_E01_079_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_079_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q. The wavefrot of a light beam is given by the equation x+2y+3z=c (where c is arbitrary constant) then the angle made by the direction of light with the y-axis is
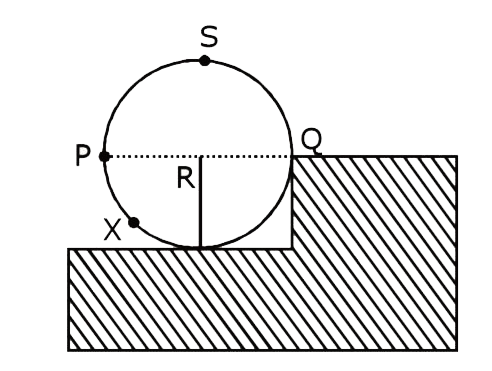
View SolutionA wheel of radius R and mass M is placed at the bottom of a fixed step of height R as shown in the figure. A constant force is continuously applied on the surface of the wheel so that it just clims the step without slipping. Consider the torque τ about an axis normal to the plane of the paper passing through the point Q. Which of the following options is/are correct?
View SolutionConsider a uniform electric field E=3×103ˆiN/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a 60∘ angle with the x-axis ?
View SolutionConsider a uniform electric field E=3×103ˆiN/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a 60∘ angle with the x-axis ?
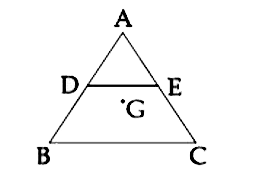
View SolutionABC is a plane lamina of the shape of an equilateral triangle. D , E are mid points of AB,AC and G is the centroid of the lamina . Moment of inertia of the lamina about an axis passing through G and perpendicular to the plane ABC is I0 If part ADE is removed, the moment of inertia of a remaining part about the same axis is NI016 where N is an integer . Value of N is
View Solution
