The masses of the block A and B are mandM Between A and B there is a constant force F but B can slide frictionlessly on the horizontal surface A is set in motion with velocity v0 while B is at rest . What is the distance moved by A relative to B before they move with the same velocity

mMv20F(m−M)
mMv202F(m−M)
mMv20F(m+M)
mMv202F(m+M)
The correct Answer is:d
Free body diagram

Equation of motion
aB=FM (in + x direction)
aA=Fm(m−xdirection)
Relative acceleration of A w.r.t, B :
¯aA,B=¯aA−¯aB=Fm=−F(m+MmM)
(along - x direction )
initial relative velocity of A w.r.t.B
aA,B=v0
Final relative velocity of A w.r.t.B = 0
Using v2=a2+2ax
0=v20−2F(m+M)nMg⇒S=Mmv202F(m+M)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Block B moves to the right with a constant velocity v0. The velocity of body a relative to b is
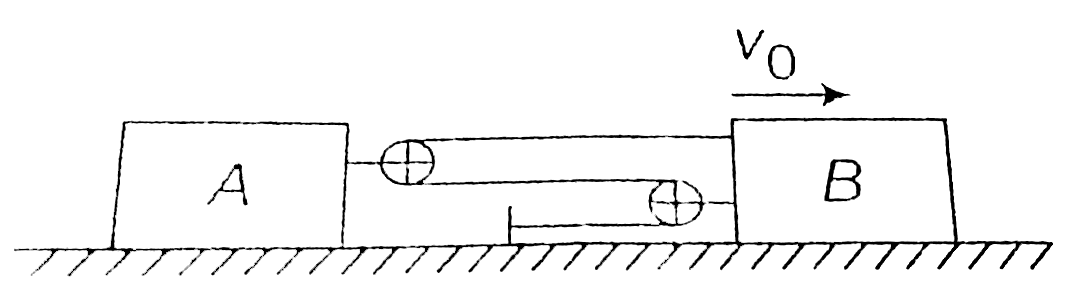
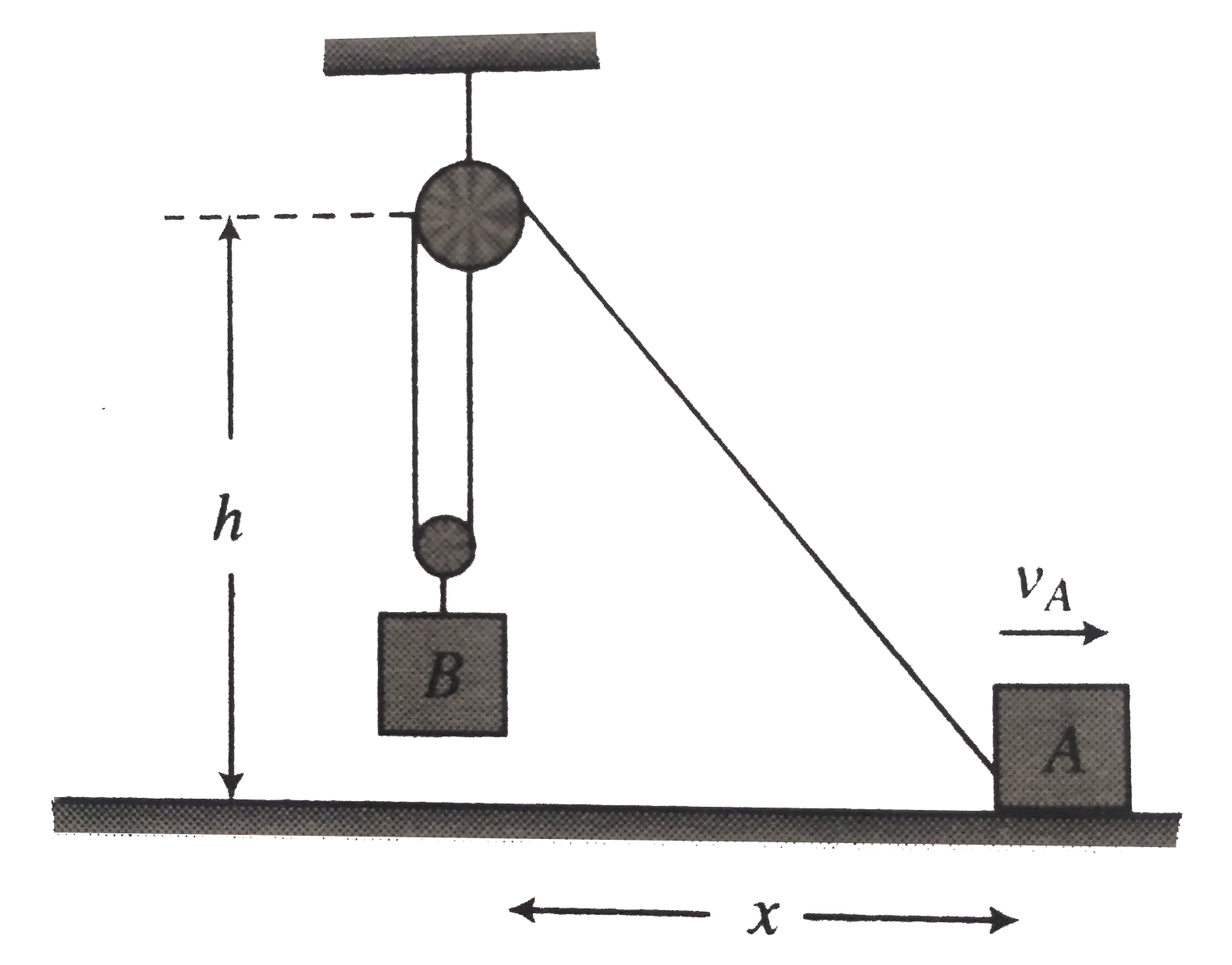
View SolutionIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: The force needed to stop them in the same
View SolutionIn the block moves up with constant velocity v m/s. Find F

View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionA block of mass m is placed on the block of mass M as shown in figure. The horizontal force →F acts on M during time interval t. If the horizontal surface is smooth, assuming no relative sliding between the blocks, find the
a. work done by friction on the blocks
b. work done by →F on the lower block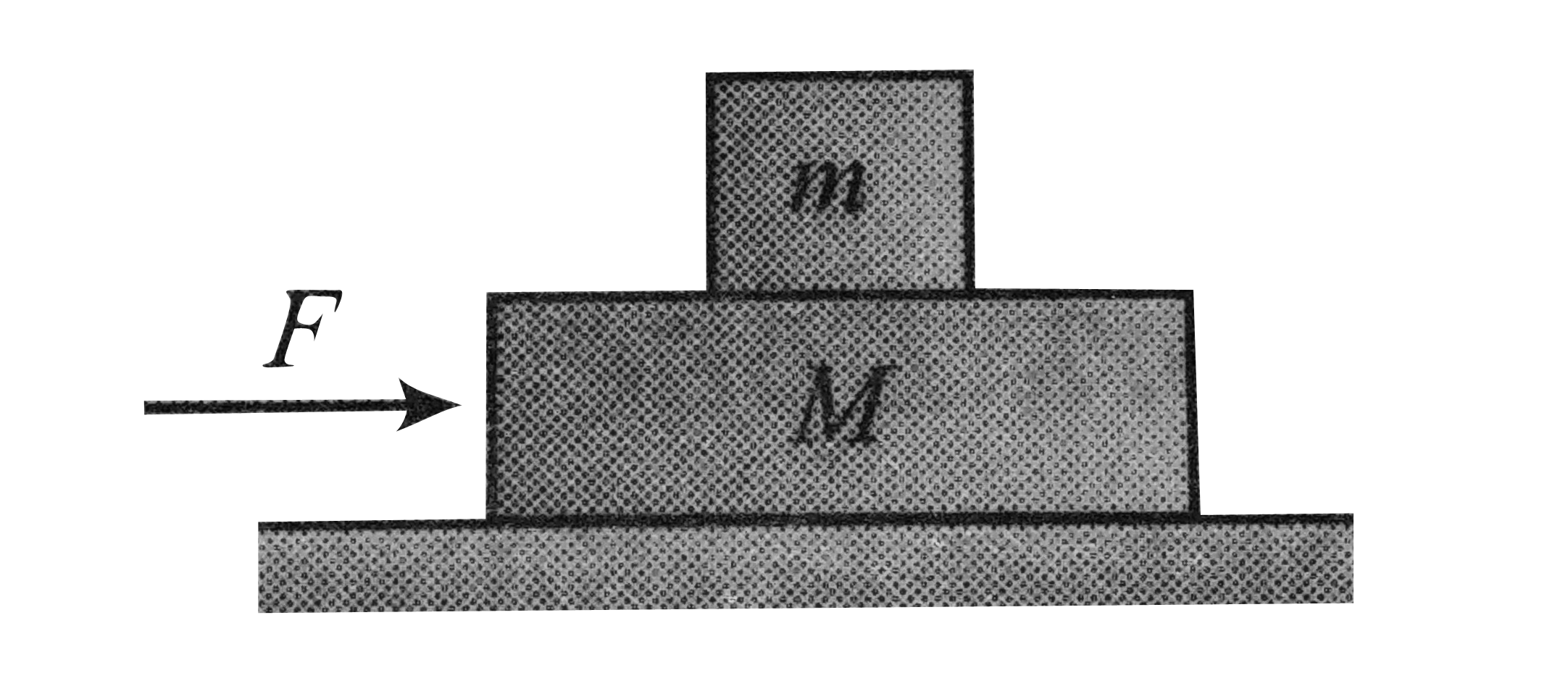
View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View Solution
