The ring M1 and block M2 are held in the position shown in fig. Now the system is released. If M1>M2, find V1/V2 wheb the ring m1 slides down along the smooth fixed vertical rod by the distance h.
To solve the problem of finding the ratio V1V2 when the ring M1 slides down a smooth vertical rod by a distance h, we can follow these steps:
1. Understanding the System:
- We have two masses: M1 (the ring) and M2 (the block).
- It is given that M1>M2.
- When the system is released, M1 will slide down the rod while M2 will move downward.
2. Defining Variables:
- Let s be the distance moved by the ring M1 along the rod.
- Let y be the distance moved by the block M2 downward.
- The length of the string connecting the two masses is constant, denoted as l.
3. Using Geometry:
- From the geometry of the situation, we can relate s, y, and l using the Pythagorean theorem:
s2=l2+y2
4. Differentiating with Respect to Time:
- Differentiate both sides of the equation with respect to time t:
2sdsdt=2ydydt
- Simplifying gives:
sdsdt=ydydt
5. Expressing Velocities:
- The velocities can be defined as:
- V1=dsdt (velocity of the ring)
- V2=dydt (velocity of the block)
- Thus, we can rewrite the equation as:
sV1=yV2
6. Finding the Ratio:
- Rearranging gives:
V1V2=ys
7. Substituting Values:
- When the ring slides down by a distance h, we have y=h.
- From the earlier relationship s2=h2+l2, we can find s:
s=√h2+l2
- Therefore, substituting y and s into the ratio gives:
V1V2=h√h2+l2
Final Result:
Thus, the ratio of the velocities is:
V1V2=h√h2+l2
- We have two masses: M1 (the ring) and M2 (the block).
- It is given that M1>M2.
- When the system is released, M1 will slide down the rod while M2 will move downward.
- Let s be the distance moved by the ring M1 along the rod.
- Let y be the distance moved by the block M2 downward.
- The length of the string connecting the two masses is constant, denoted as l.
- From the geometry of the situation, we can relate s, y, and l using the Pythagorean theorem:
s2=l2+y2
- Differentiate both sides of the equation with respect to time t:
2sdsdt=2ydydt
- Simplifying gives:
sdsdt=ydydt
- The velocities can be defined as:
- V1=dsdt (velocity of the ring)
- V2=dydt (velocity of the block)
- Thus, we can rewrite the equation as:
sV1=yV2
- Rearranging gives:
V1V2=ys
- When the ring slides down by a distance h, we have y=h.
- From the earlier relationship s2=h2+l2, we can find s:
s=√h2+l2
- Therefore, substituting y and s into the ratio gives:
V1V2=h√h2+l2
Thus, the ratio of the velocities is:
V1V2=h√h2+l2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
Similar Questions
Two blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
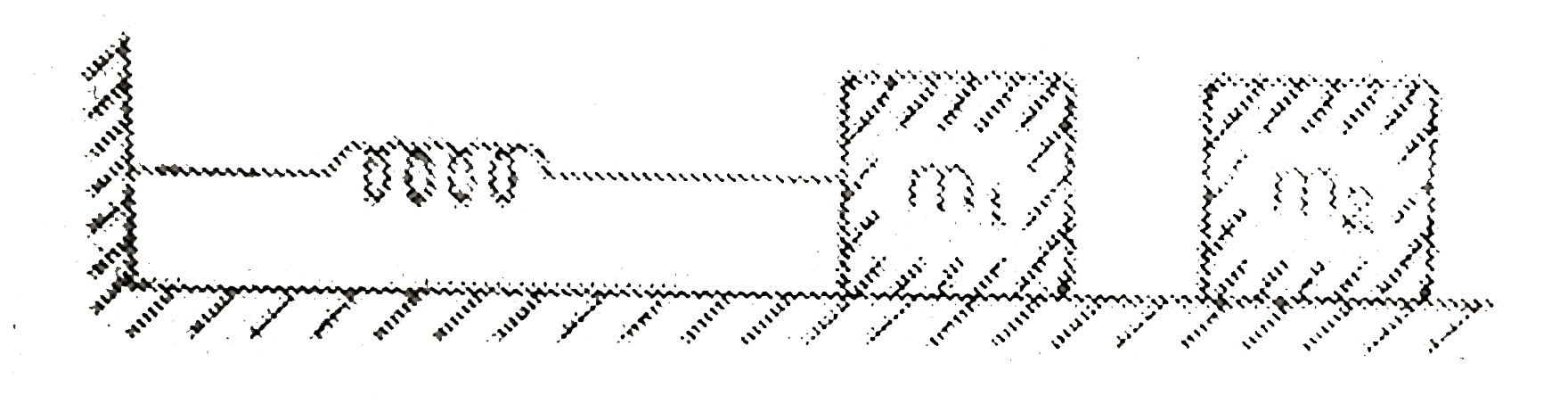
View SolutionUse of dilution formula (M1V1=M2V2)

View SolutionThree blocks are connected as shown in fig. on a horizontal frictionless table if m1=1kg,m2=8kg,m3=27kg and T3=36N,T2 will be:-

View SolutionTwo point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.
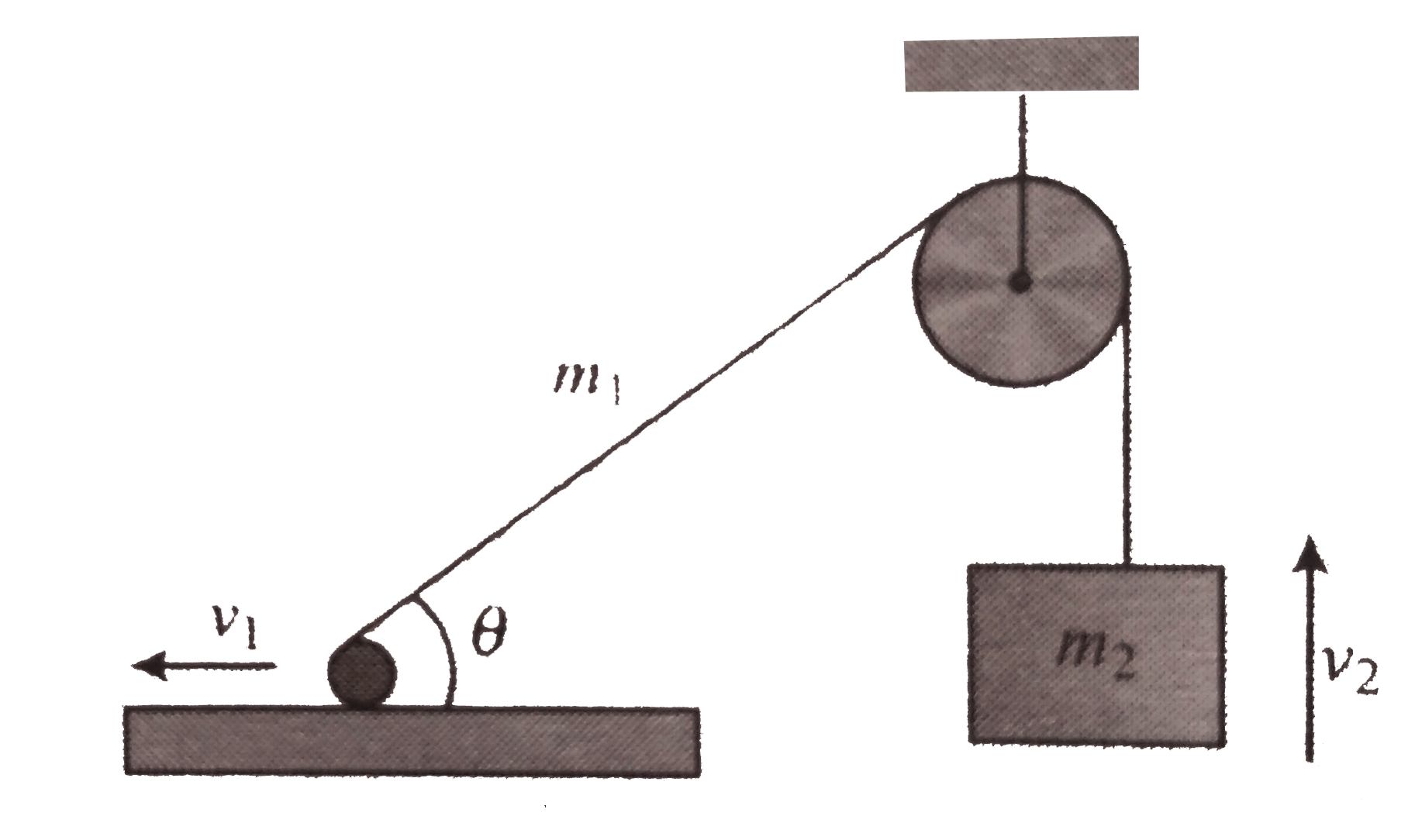
View SolutionIn fig. a ball of mass m1 and a block of mass m2 are joined together with an inextensible string. The ball can slide on a smooth horizontal surface. If v1 and v2 are the respective speeds of the ball and the block, then determine the constraint relation between the two.
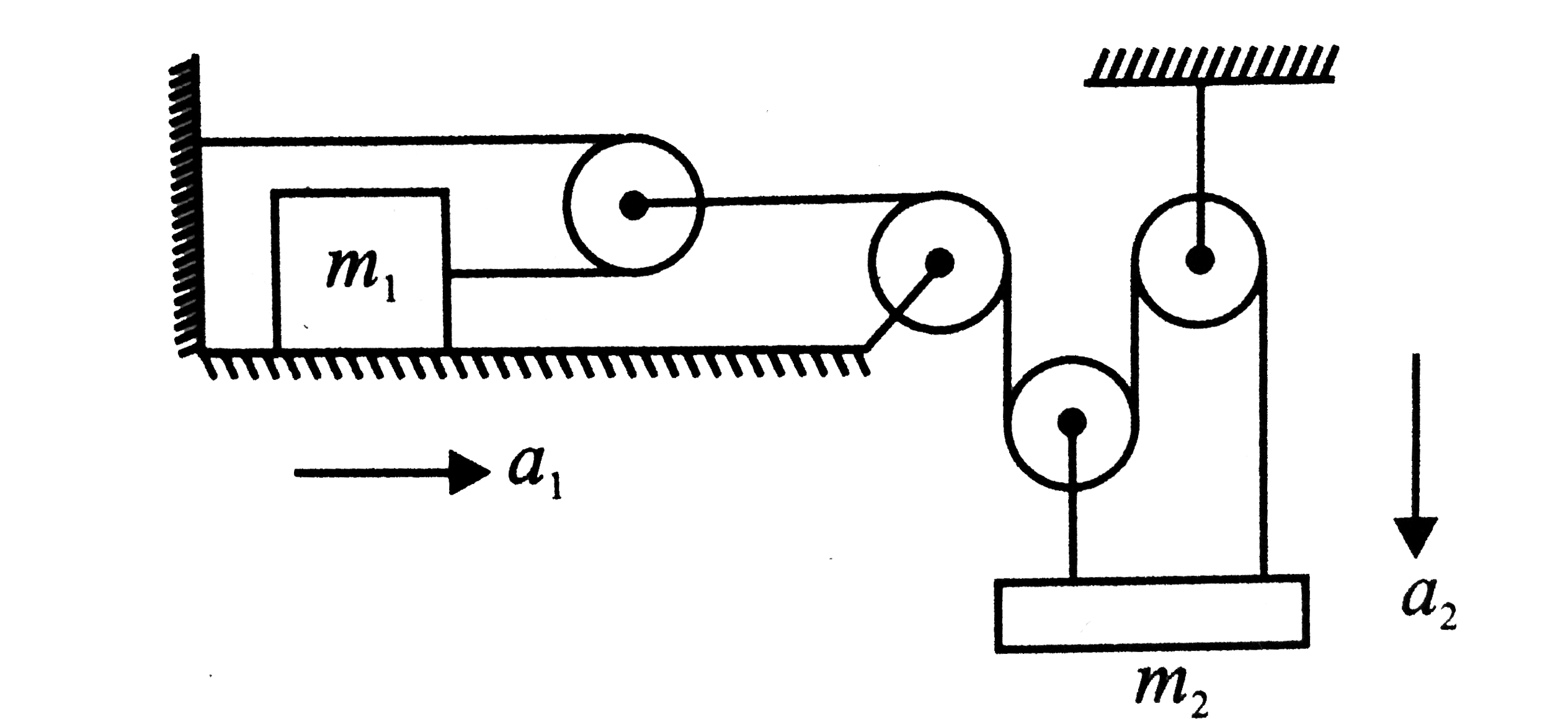
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View SolutionFor the system shown in fig, there is no friction anywhere. Masses m1andm2 can move up or down in the slots cut in mass M. Two non-zero horizontal force F1 and F2 are applied as shown. The pulleys are massles and frictionless. Given m1≠m2

Let F1 and F2 are applied in such a way that m1andm2 do not move w.r.t. M. then what is the magnitude of the acceleration of M? Let m1>m2.
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionIn the fig. m2>m1. Pulley and string and massless and Pulley is smooth. The system is released from rest. After 2 seconds of motion m2 was held with the hand.

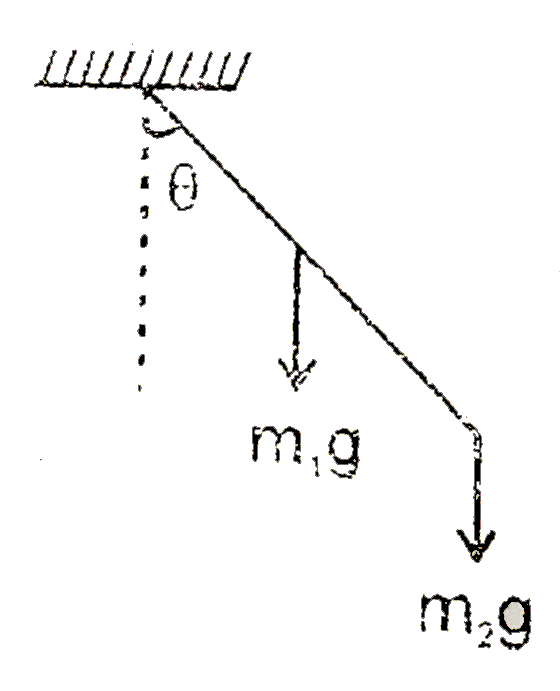
View SolutionA mass m1 lies on fixed, smooth cylinder . An ideal cord attached to m1 passes over the cylinder and is connected to mass m2 as shown in the figure.
(a) Find the value of θ( shown in diagram ) for which the system is in equilibrium.
(b) Given m1=5kg,m2=4kg . The system is released from rest when θ=30∘ . Find the magnitude of acceleration of mass m1 just after the system is released.

View Solution
