A mass m1 lies on fixed, smooth cylinder . An ideal cord attached to m1 passes over the cylinder and is connected to mass m2 as shown in the figure.
(a) Find the value of θ( shown in diagram ) for which the system is in equilibrium.
(b) Given m1=5kg,m2=4kg . The system is released from rest when θ=30∘ . Find the magnitude of acceleration of mass m1 just after the system is released.

The correct Answer is:sinθ=m2m1
(b)159m/s2
(a) The system is in equilibrium when m1gsinθ=m1g
or sinθ=m2m1
(b) Let the tangential acceleration of m1 be a.
∴m2g−m1gsinθ=(m1+m2)a
a=40−259=159m/s2
the normal acceleration of m1 is zero.
∵ speed of m1 is zero.
∴ The magnitude of acceleration of m1=53m/s2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 83
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 84
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 81
4 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A mass m1 lies on a fixed smooth cylinder. An ideal chord attached to m1 passes over the cylinder and is conneced to m2. The system is released at θ=30∘. Acceleration of m1 just after releasing the system is 5nm/s2. Find the value of n.
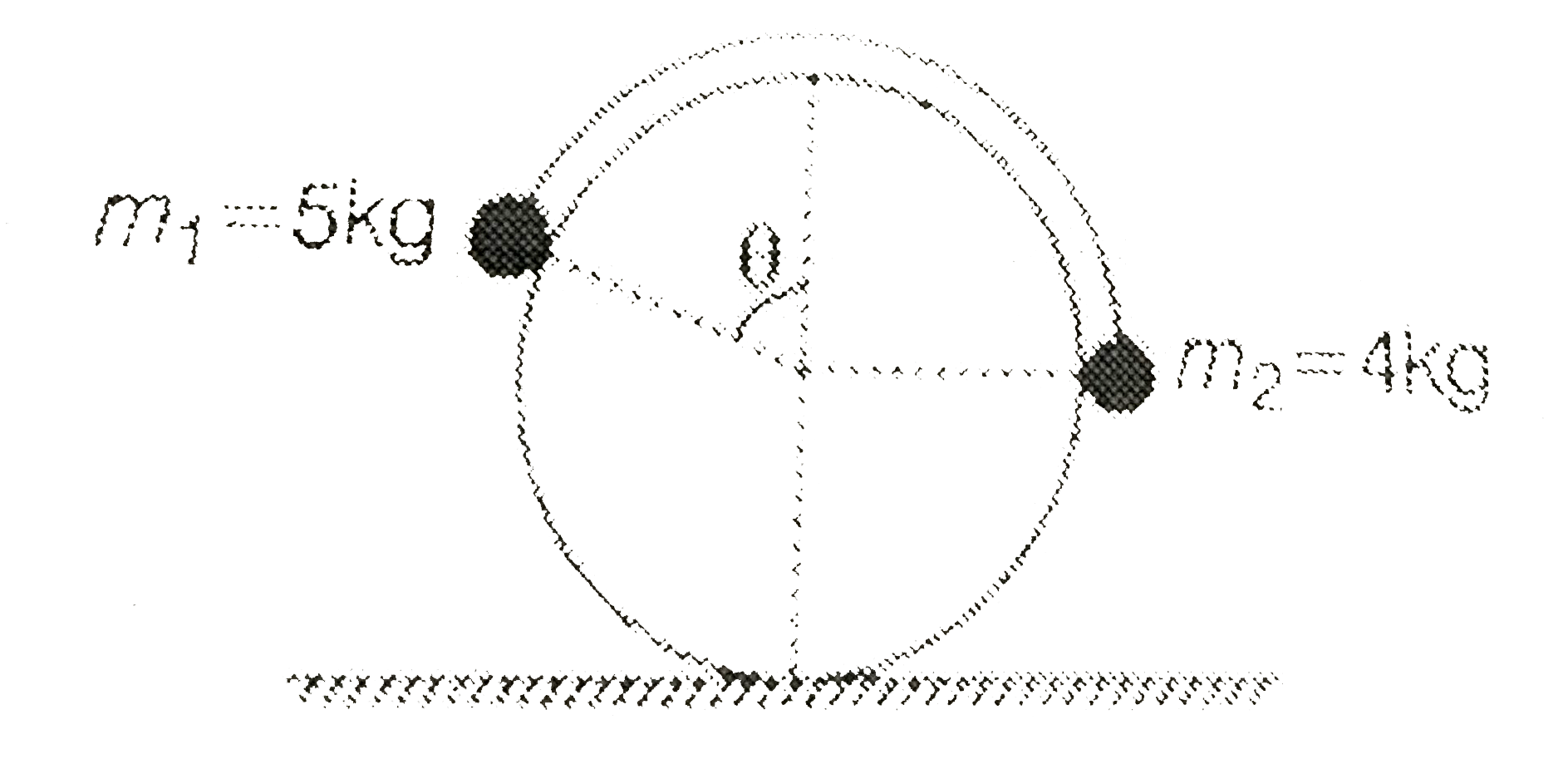
View SolutionA mass 2m lies on a fixed , smooth cylinder . An ideal string attached to 2m passes over the cylinder to mass m . Then the value of angle θ for which system is in equilibrium
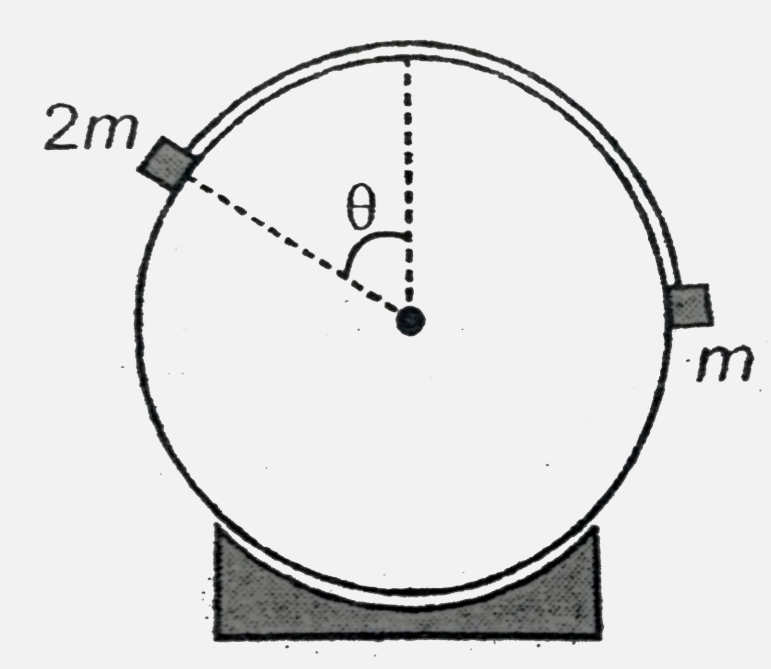
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
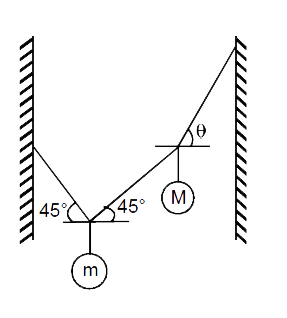
View SolutionThe system is released from rest. All surface are smooth . Find the angle theta at which the acceleration of wedge is maximum. ( given .Mm=12)
View SolutionA block of mass m1 on asmooth, horizontal surface is connected to a second mass m2 by a light string over a height, frictionless pulley. A force of magnitude F0 is applied to mass m1. Find the value of force F0 for which the system will be is equilibrium.

View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.

View SolutionA block B of mass M is suspended from a cord of length l attached to a cart A of mass M as shown in the figure. The horizontal surface on which the cart moves is smooth. Initially both the cart and the block are at rest in the position shown. Now B is released. Take M=m=2kg,θ=45∘andg=10m/s2.
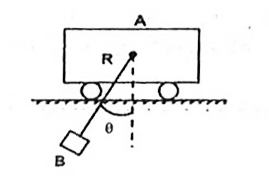
The magnitude of acceleration of B (with respect to cart) immediately after the system is released from rest is
View SolutionConsider the system of masses and pulleys shown in fig. with massless string and fricitionless pulleys.
(a) Give the necessary relation between masses m1 and m2 such that system is in equilibrium and does not move.
(b) If m1=6kg and m2=8kg, calculate the magnitude and direction of the acceleration of m1.
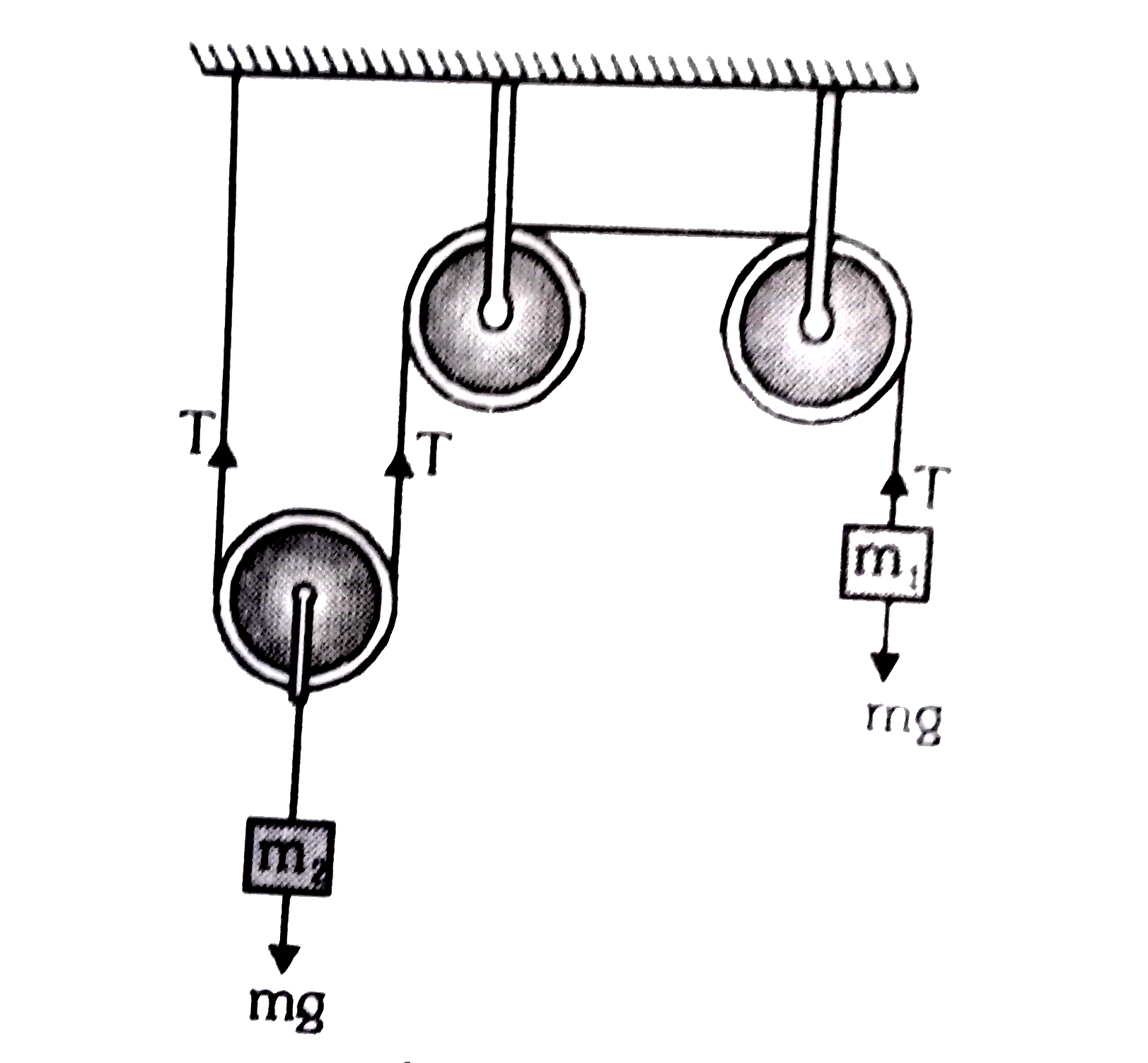
View SolutionBlocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
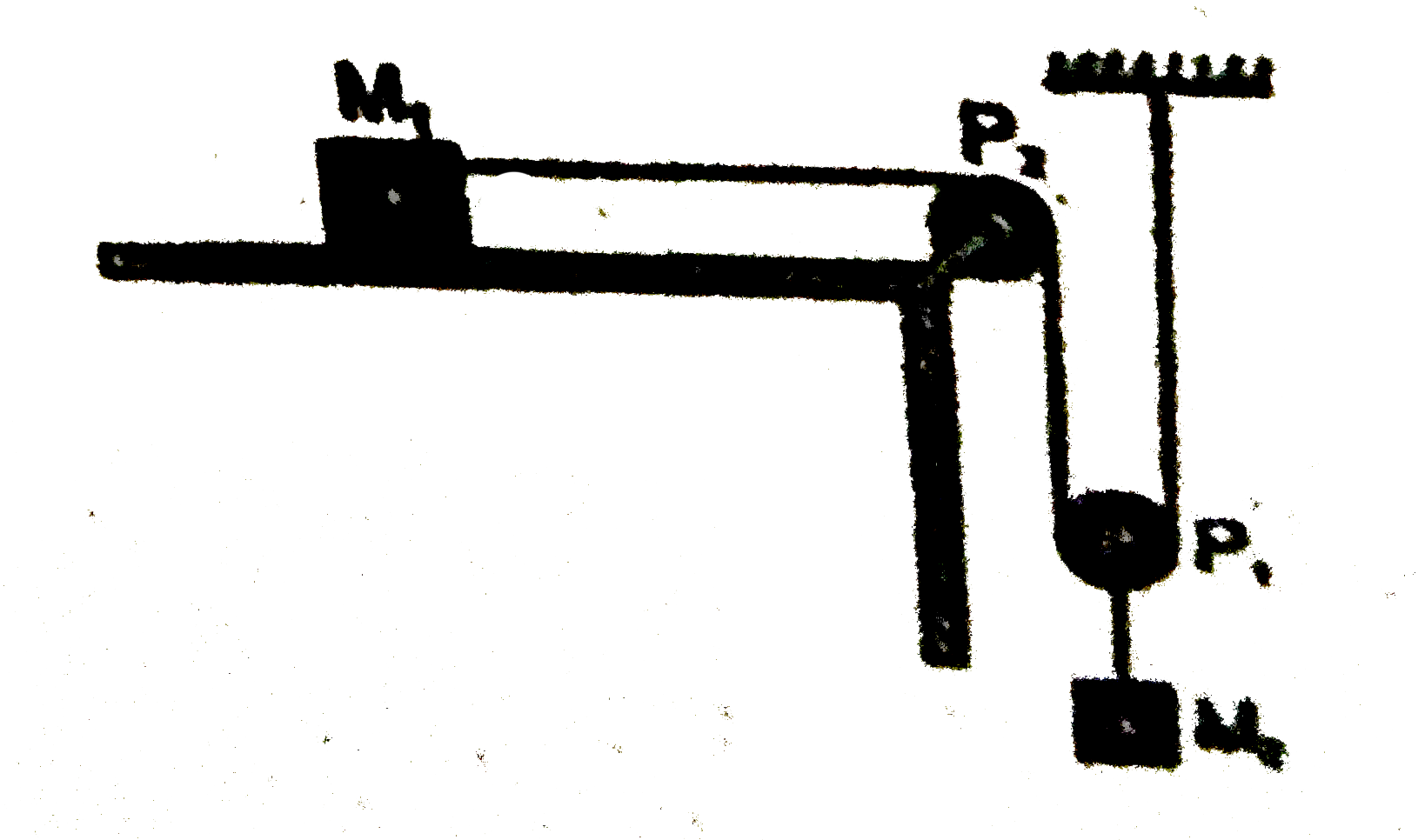
View SolutionThe blocks A and B shown in figure have masses MA=5kg and MB=4kg. The system is released from rest. The speed of B after A has travelled a distance 1m along the incline is
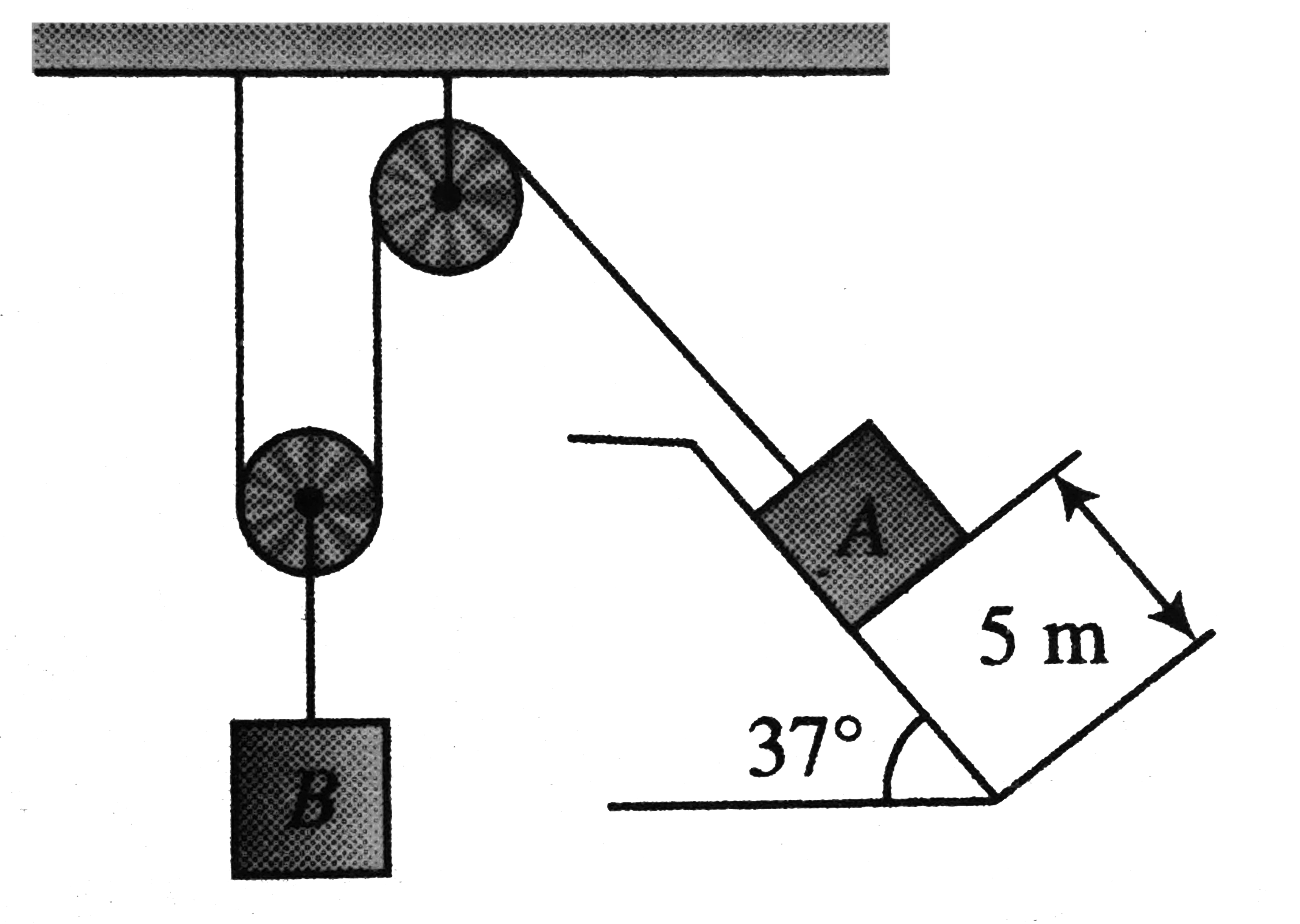
View Solution
