A ball is thrown from a point in level with velocity $u$ and at a horizontal distance $r$ from the top os a tower of height $h$ .
At what horizontal distance $x$ from the foot of the tower does the ball hit the ground ?

A

$\frac{u \cos θ}{g} {{(u^{2} \sin^{2} θ + g h)}^{1 / 2} - u \sin θ}$

B

$\frac{u \cos θ}{g} {{(u^{2} \cos^{2} θ + 2 g h)}^{1 / 2} - u \cos θ}$

C

$\frac{u \cos θ}{g} {{(u^{2} \cos^{2} θ + g h)}^{1 / 2} - u \cos θ}$

D

$\frac{u \cos θ}{g} {{(u^{2} \cos^{2} θ + g h)}^{1 / 2} - u \cos θ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

( a) Here $r$ will become range
$r = \frac{u^{2} \sin 2 θ}{g}$
$\Rightarrow g r = u^{2} \sin 2 θ$
$h = u \sin θ t + \frac{1}{2} {gt}^{2}$
$x = u \cos θ t$
$t = \frac{x}{u \cos θ}$
$h = u \sin θ \frac{x}{u \cos θ} + \frac{1}{2} \frac{g (x^{2})}{u^{2} \cos^{2} θ}$
$g x^{2} + 2 u^{2} \sin θ \cos θ x - 2 h u^{2} \cos^{2} θ = 0$
$x = \frac{u \cos θ}{g} [\sqrt{u^{2} \sin^{2} θ + 2 g h - u \sin θ}]$ .
.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

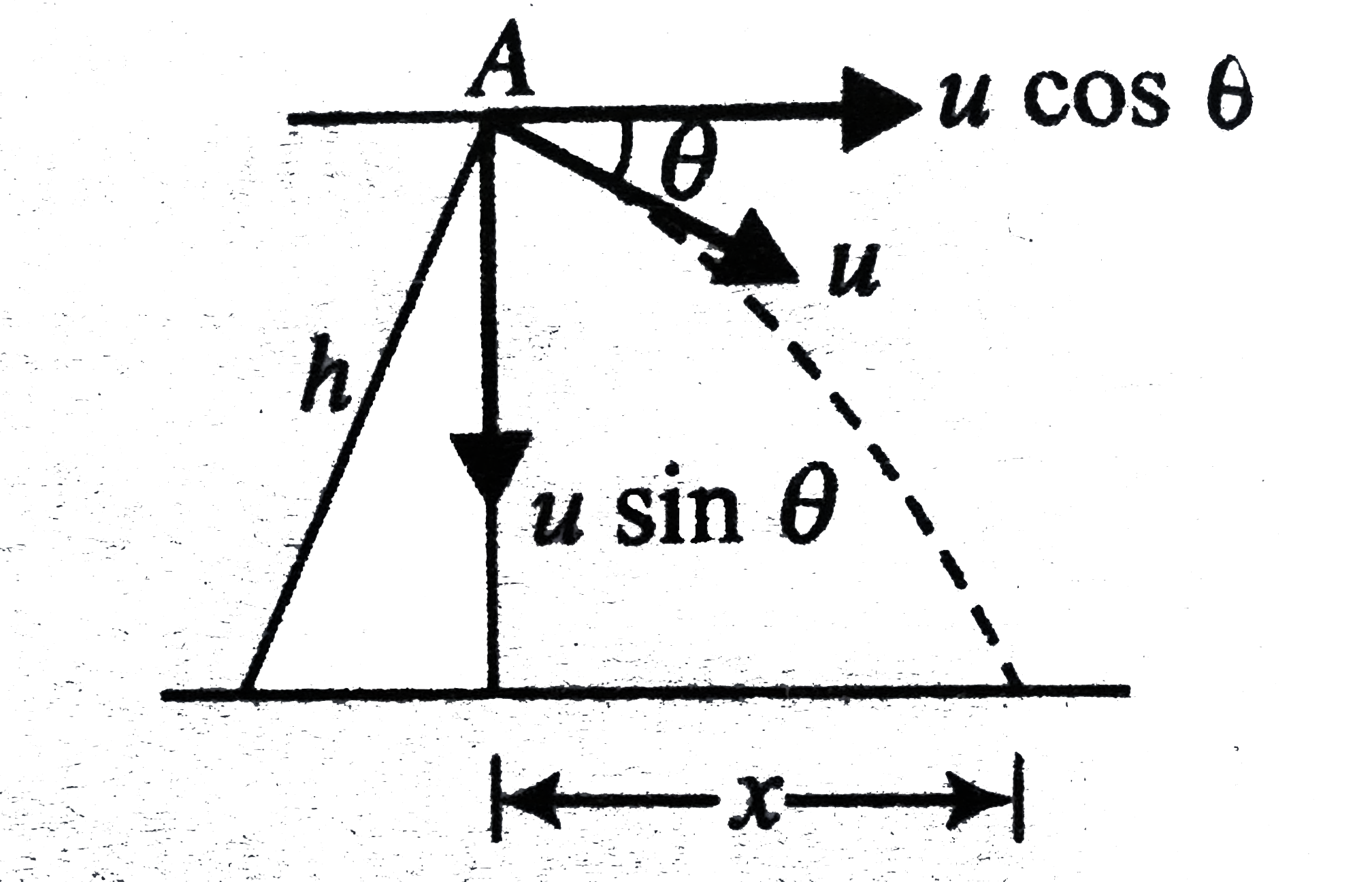Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A body of mass m thrown horizontally with velocity v, from the top of tower of height h touches the level ground at a distance of 250m from the foot of the tower. A body of mass 2m thrown horizontally with velocity $v / 2$ , from the top of tower of height 4h will touch the level ground at a distance x from the foot of tower. The value of x is
A250 m
B500 m
C125 m
D $250 \sqrt{2}$ m

CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Exercise Comprehension

Home
Ask Doubt
Profile