A projectile is thrown into space so as to have maximum horizontal range R. Taking the point of projection as origin, find out the co-ordinates of the point where the speed of the particle is minimum.
To find the coordinates of the point where the speed of the projectile is minimum, we can follow these steps:
Step 1: Understand the projectile motion
A projectile thrown at an angle will have both horizontal and vertical components of velocity. The horizontal component remains constant, while the vertical component changes due to gravity.
Step 2: Determine the angle for maximum range
For maximum horizontal range R, the angle of projection θ is 45∘. This is a key point because it will help us in calculating the components of the initial velocity.
Step 3: Components of initial velocity
Let the initial speed of the projectile be u. The components of the initial velocity can be expressed as:
- Horizontal component: ux=ucos(45∘)=u√2
- Vertical component: uy=usin(45∘)=u√2
Step 4: Time of flight
The total time of flight T for a projectile is given by:
T=2uyg=2⋅u√2g=u√2g
Step 5: Vertical position as a function of time
The vertical position y of the projectile at any time t is given by:
y(t)=uyt−12gt2=u√2t−12gt2
Step 6: Horizontal position as a function of time
The horizontal position x of the projectile at any time t is given by:
x(t)=uxt=u√2t
Step 7: Speed of the projectile
The speed v of the projectile at any point in time can be calculated using the components of velocity:
v=√v2x+v2y
Where:
- vx=ux=u√2 (constant)
- vy=uy−gt=u√2−gt
Step 8: Finding the minimum speed
The speed will be minimum when the vertical component vy is zero (i.e., when the projectile reaches its maximum height). Setting vy=0:
u√2−gt=0⟹t=ug√2
Step 9: Calculate the coordinates at this time
Substituting t into the equations for x(t) and y(t):
- x(ug√2)=u√2⋅ug√2=u22g
- y(ug√2)=u√2⋅ug√2−12g(ug√2)2
=u22g−12g⋅u22g2=u22g−u24g=u24g
Final Coordinates
Thus, the coordinates of the point where the speed of the projectile is minimum are:
(u22g,u24g)
A projectile thrown at an angle will have both horizontal and vertical components of velocity. The horizontal component remains constant, while the vertical component changes due to gravity.
For maximum horizontal range R, the angle of projection θ is 45∘. This is a key point because it will help us in calculating the components of the initial velocity.
Let the initial speed of the projectile be u. The components of the initial velocity can be expressed as:
- Horizontal component: ux=ucos(45∘)=u√2
- Vertical component: uy=usin(45∘)=u√2
The total time of flight T for a projectile is given by:
T=2uyg=2⋅u√2g=u√2g
The vertical position y of the projectile at any time t is given by:
y(t)=uyt−12gt2=u√2t−12gt2
The horizontal position x of the projectile at any time t is given by:
x(t)=uxt=u√2t
The speed v of the projectile at any point in time can be calculated using the components of velocity:
v=√v2x+v2y
Where:
- vx=ux=u√2 (constant)
- vy=uy−gt=u√2−gt
The speed will be minimum when the vertical component vy is zero (i.e., when the projectile reaches its maximum height). Setting vy=0:
u√2−gt=0⟹t=ug√2
Substituting t into the equations for x(t) and y(t):
- x(ug√2)=u√2⋅ug√2=u22g
- y(ug√2)=u√2⋅ug√2−12g(ug√2)2
=u22g−12g⋅u22g2=u22g−u24g=u24g
Thus, the coordinates of the point where the speed of the projectile is minimum are:
(u22g,u24g)
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
25 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.3
12 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A projectile is thrwon into space so as to have the maximum possible horizontal range equal to 400m. Taking the point of projection as the origin, the coordinates of the point where the velocity of the projectile is minimum are:-
View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.
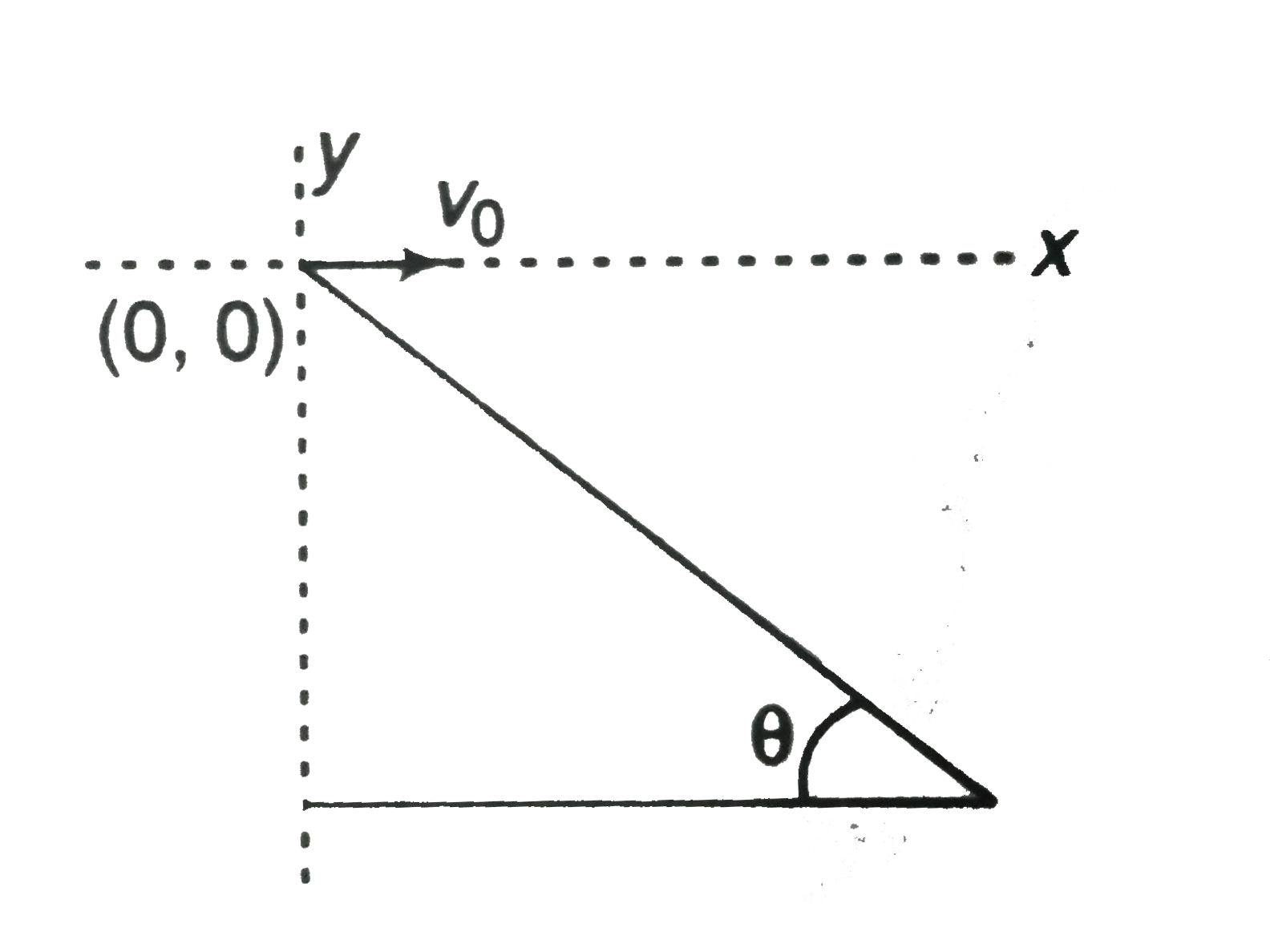
View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.

View SolutionAt which point should the origin be shifted so that co-ordinates of point (2,5) become (1,−4) ?
View SolutionA particle is projected from ground at some angle with horizontal (Assuming point of projection to the origin and the horizontal and vertical directions to be the x and y axis) the particle passes through the points (3, 4) m and (4, 3) m during its motion then the range of the particle would be : (g=10m/s2)
View SolutionThe co-ordinates of two points A and B are (-3, 4) and (2, -1). Find :
the co-ordinates of the point where the line AB intersects the y-axis.
View SolutionIf a particle of mass m is thrown with speed at an angle 60° with horizontal, then angular momentum of particle at highest point about point of projection is
View SolutionA projectile, thrown with velocity v0 at an angle α to the horizontal, has a range R. it will strike a vertical wall at a distance R/2 from the point of projection with a speed of
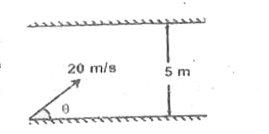
View SolutionA projectile is projected with a speed = 20 m/s from the floor of a 5 m high room as shown. Find the maximum horizontal range of the projectile and the corresponding angle of projection θ.
View SolutionA body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.
View Solution
