A point move with uniform acceleration and υ1,υ2 and υ3 denote the average velocities in the three successive intervals of time t1,t2 and t3. which of the following relations is correct ?
(v1−v2):(v2−v3=(t1−t2:(t2+t3.
(v1−v2):(v2−v3=(t2−t2:(t2+t3
(v1−v2):(v2−v3=(t1−t2:(t2+t3
(v1−v2):(v2−v3=(t1−t2:(t2+t3
The correct Answer is:B
Suppose u be the initial velocity.
Velocity after time t1: v11=u+at1
Velocity after time t1+t2: v22=u+a(t1+t2
Velocity after time t1+t2+t3:
v3=u+a(t1+t2+t3)
Now v1=u+v112=u+u+at12=u+12at1
v2=v11+v222=u+at1+122
v3=v33+v332=u+at2+12at3
So v1−v2=−12a(t1+t2)
v2−v3=−12a(t2−t3)
(v1−v2): (v2−v3=(t1+t2) : (t2+t3).
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective
29 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle moving with uniform acceleration has average velocities ν1,ν2 and ν3 over the successive intervals of time t1,t2 and t3 respectively. The value of ν1−ν2ν2−ν3 will be
View SolutionA particle moves in x-y plane and at time t is at the point (t2,t3−2t), then which of the following is/are correct?
View Solution
Knowledge Check
A point moves with a uniform acceleration and v1,v2,v3 denote the average velociies in the three succellive intervals of time t1 ,t2 and t3. Find the ratio of ( v1 - v2) and ( v2 - v3).
At1−t2t2−t3Bt1−t3t2+t3Ct1+t2t2−t3Dt1+t2t2+t3
Find the average velocity for the time intervals Δt=t2−0.75 when t2 is 1.75 ,1.25 and 1.0 s. What is the instantaneous velocity at t=0.75 s?
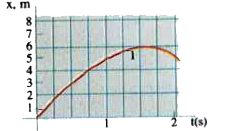
View Solution
A disc is rolling (without slipping) on a horizontal surface. C is its centre and Q and P are two point equidistance from C. let υp,υQ and υC be the magnitude of velocities of points P, Q, and C repsectively,
(a). υQ>υC>υP
(b). υQ<υC<υP
(c). υQ=υP,υC=12υP
(d). υQ<υC>υP
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View SolutionThe initial velocity of a particle is x ms−1 (at t=0) and acceleration a is function for time, given by, a= 6t. Which of the following relation is correct for final velocity y after time t?
View SolutionA point traversed 3/4 th of the circle of radius R in time t. The magnitude of the average velocity of the particle in this time interval is
View SolutionGraph of velocity (v) versus time 't' for motion of a motorbike which starts from rest and moves along a stright road is given .
(a)Find the average acceleration for the time interval t0=0 to t1=6.0 s
(b) Estimate the time at which the acceleration has its greatest positive value and the value of the acceleration at that instant.
(c) When is the acceleration is zero ?
(d) Estimate the maximum negative value of the acceleration and the time at which it occurs.
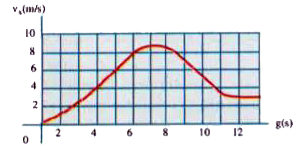
View SolutionA body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
View Solution
