A point traversed 3/4 th of the circle of radius R in time t. The magnitude of the average velocity of the particle in this time interval is
πRt
3πR2t
R√2t
R√2t
The correct Answer is:C
To find the magnitude of the average velocity of a particle that traverses 3/4 of a circle of radius R in time t, we can follow these steps:
1. Understand the Motion: The particle travels along the circumference of a circle. Given that it covers 3/4 of the circle, we need to identify the initial and final positions of the particle.
2. Identify Initial and Final Points:
- Let's denote the center of the circle as point O.
- Assume the particle starts at point A (0 degrees) and moves to point B (270 degrees) after covering 3/4 of the circle.
3. Determine Displacement:
- Displacement is defined as the shortest distance between the initial and final points.
- The initial point A is at coordinates (R, 0) and the final point B is at coordinates (0, -R).
4. Calculate the Displacement Vector:
- The displacement vector from A to B can be calculated as:
Displacement=Final Position−Initial Position=(0,−R)−(R,0)=(−R,−R)
5. Calculate the Magnitude of Displacement:
- The magnitude of the displacement can be found using the Pythagorean theorem:
Magnitude of Displacement=√(−R)2+(−R)2=√R2+R2=√2R2=R√2
6. Calculate Average Velocity:
- Average velocity is defined as the total displacement divided by the total time taken:
Average Velocity=Total DisplacementTotal Time=R√2t
Final Answer:
The magnitude of the average velocity of the particle is:
R√2t
- Let's denote the center of the circle as point O.
- Assume the particle starts at point A (0 degrees) and moves to point B (270 degrees) after covering 3/4 of the circle.
- Displacement is defined as the shortest distance between the initial and final points.
- The initial point A is at coordinates (R, 0) and the final point B is at coordinates (0, -R).
- The displacement vector from A to B can be calculated as:
Displacement=Final Position−Initial Position=(0,−R)−(R,0)=(−R,−R)
- The magnitude of the displacement can be found using the Pythagorean theorem:
Magnitude of Displacement=√(−R)2+(−R)2=√R2+R2=√2R2=R√2
- Average velocity is defined as the total displacement divided by the total time taken:
Average Velocity=Total DisplacementTotal Time=R√2t
The magnitude of the average velocity of the particle is:
R√2t
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.3
Explore 10 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.4
Explore 15 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.1
Explore 10 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
A particle travels two and a half revolutions of the circle of radius R in time t. The ratio of the average speed of the particle to the magnitude of the average velocity in this time interval is
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View SolutionFigure shows the velocity time graph for a particle travelling along a straight line. The magnitude of average velocity (in m/s) of particle during the time interval from t=0 to t=6s is 10α. Find the value of α.
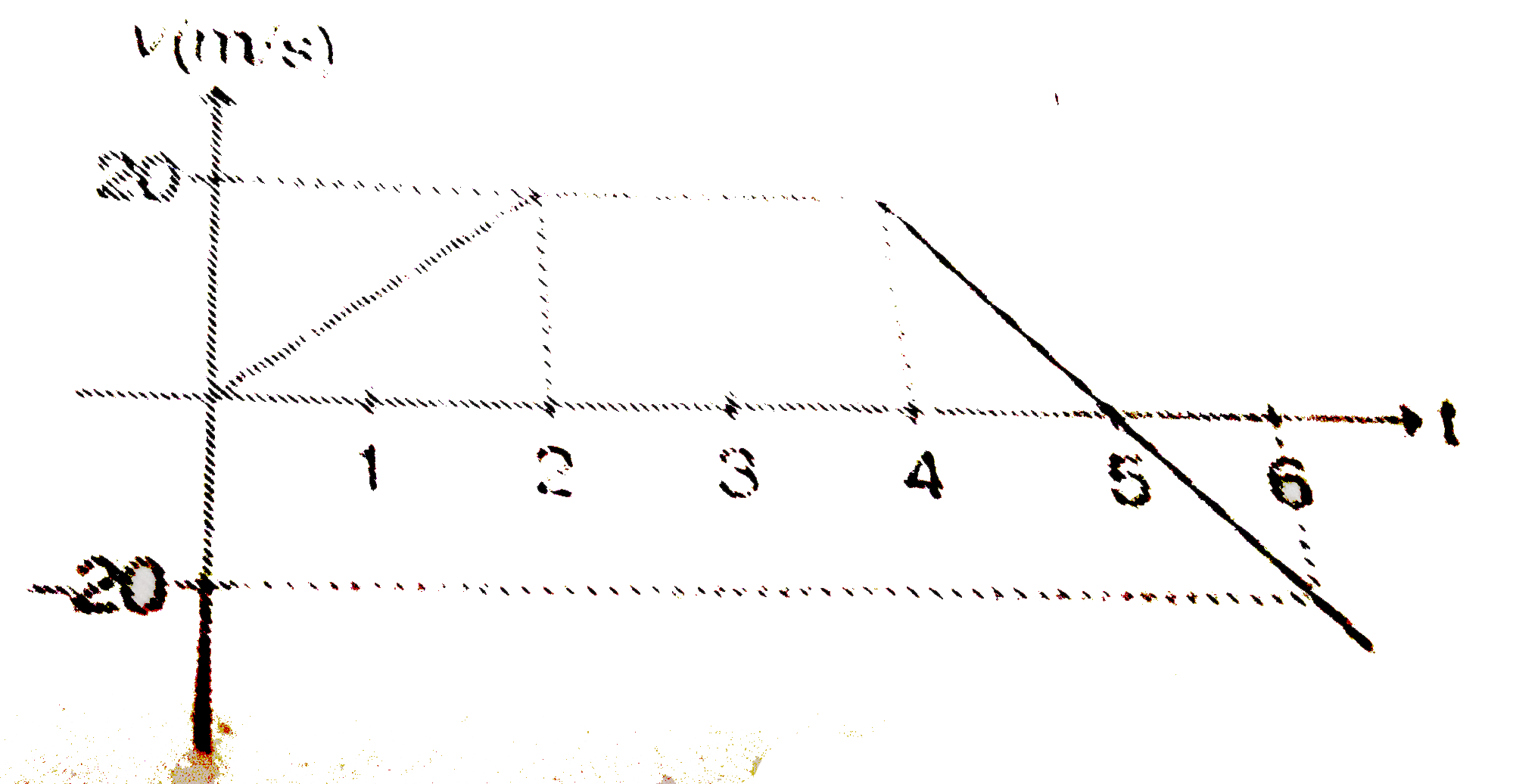
View SolutionA particle is projected from ground with speed 80 m/s at an angle 30∘ with horizontal from ground. The magnitude of average velocity of particle in time interval t = 2 s to t = 6 s is [Take g = 10 m/s2]
View SolutionA particle is moving with speed v in a circle of radius R. Find the magnitude for average velocity of point
for the half revolution
View SolutionStarting from rest, a particle rotates in a circle of radius R = √2m with an angular acceleration = π4 rad/s2.The magnitude of average velocity of the particle over the time it rotates quarter circle is:
View SolutionIf magnitude of average speed and average velocity over a time interval are same, then
View SolutionThe velocity time graph of a particle moving along a straight line is shown in the figure. In the time interval from t=0 to t=8 second, answer the following three question.

The value of magnitude of maximum velocitymagnitude of average velocity for the given time interval is :
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View Solution
