Between two stations a train starting from rest first accelerates uniformly, then moves with constant velocity and finally retarts uniformly to come to rest. If the ratio of the time taken be and the maximum speed attained be , then what is the average speed over the whole journey ?
The correct Answer is:C
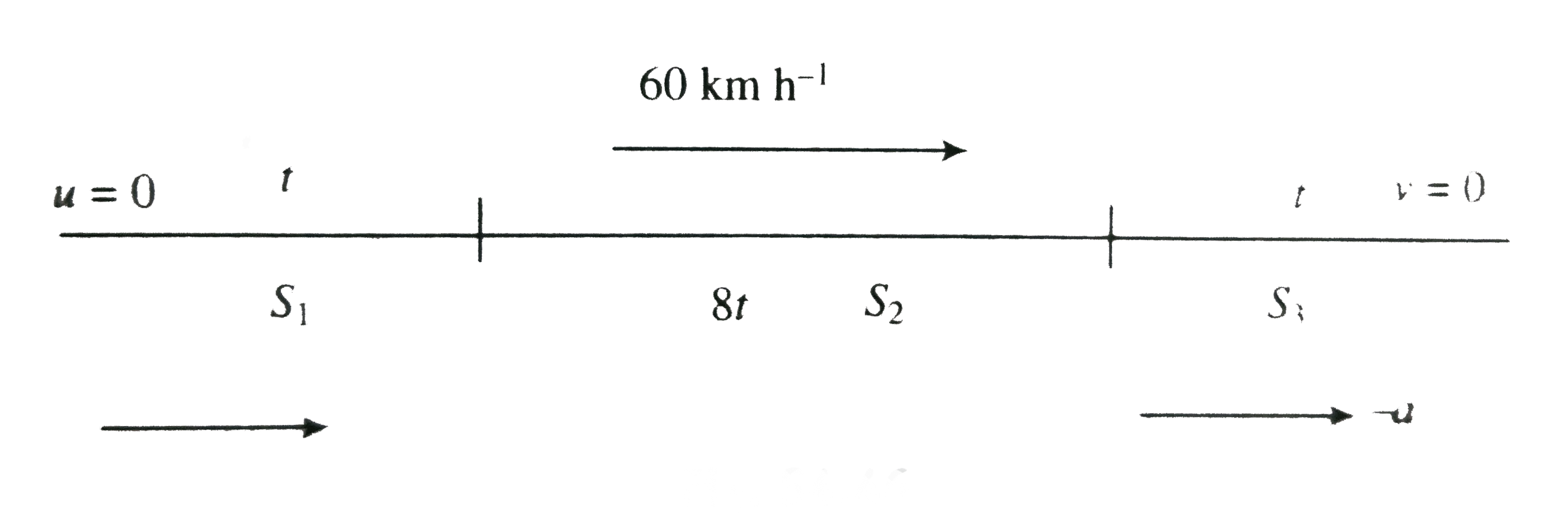 .
.
.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept17videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept1videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective29videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
A body starts from rest with an acceleration 2m/s2 till it attains the maximum velocity then retards to rest with 3m/s2. If total time taken is 10 second, then maximum speed attained is
View SolutionA car acceleration from rest at a constant rate 2m/s2 for some time. Then, it retards at a constant rate of 4m/s2 and comes to rest. If it remains motion for 3 second, then the maximum speed attained by the car is:-
View SolutionA car moves for half of its time at 80 km/h and for rest half of time at 40 km/h. Total distance covered is 60 km. What is the average speed of the car
View SolutionA car moves for half of its time at 80km/h and for rest of time at 40km/h. Total distance covered is 60km. What is the average speed of the car
View SolutionA bus starting from rest, accelerates at the rate of f through a distance S, then continues at constant speed for time t and declerates at the rate f/2 to come to rest. If the total distance travelled is 15 S then S =
View SolutionA car, starting from rest, accelerates at the rate f through a distance s, then continues at constant speed for time t and then decelerates at the rate f/ 2 to come to rest. If the total distance travelled is 15 s, then
View SolutionA car, starating from rest, accelerates at the rate f through a distance S, then continoues at constant speed for time t and then decelerates as the rate f/2 to come to rest. If the total distance travelled is 15 S, then
View SolutionA particle starts from rest and traverses a distance l with uniform acceleration, then moves uniformly over a further distance 2l and finally comes to rest after moving a further distance 3l under uniform retardation. Assuming entire motion to be rectilinear motion the ratio of average speed over the journey to the maximum speed on its ways is
View SolutionIf the first one - third of q journey is travelled at 20 km h−1 , Next one - third at 40kmh−1 And the last one third at 60kmh−1 then the average speed for the whole journey will be
View SolutionA train accelerates from rest at a constant rate a for time t1and then it retards at the constant rate b for time t2 then comes to rest. Find the ratio t1/t2.
View Solution


