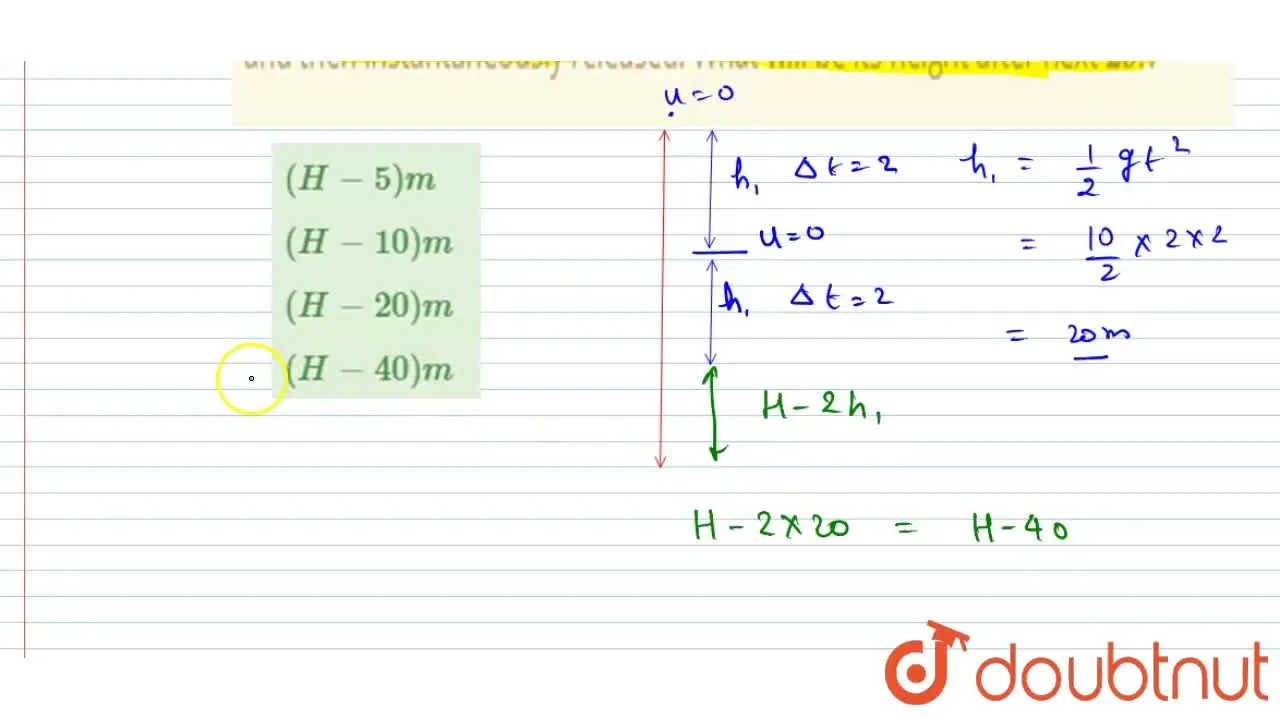
A ball is released from the top of a tower of height Hm. After 2s is stopped and then instantaneously released. What will be its height after next 2s?.
(H−5)m
(H−10)m
(H−20)m
(H−40)m
The correct Answer is:D
Distance covered by by the object in first 2s
h1=12gt2=12×10×22=20m
Similarly , destance covered by the object invext 2s will also be 20m, hence the required height =H−20−20=H−40m.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept17videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept1videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective29videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
A ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA body is released from the top of a tower of height h and takes 'T' sec to reach the ground. The position of the body at T/2 sec is
View SolutionA body is released form the top of a tower of height h meters. It takes t seconds to reach the ground. Where is the ball at the time t/2 sec ?
View SolutionA stone is released from the top of a tower of height 19.6m. Calculate its final velocity just before touching the ground.
View SolutionA body released from the top of a tower of height h takes T seconds to reach the ground. The position of the body at T/4 seconds is
View SolutionThe balls are released from the top of a tower of heigh H at regular interval of time. When first ball reaches at the grund, the nthe ball is to be just released and (n+1)2th
ball is at some distance h from top of the tower. Find the value of h.View SolutionA particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.
View Solution