Question

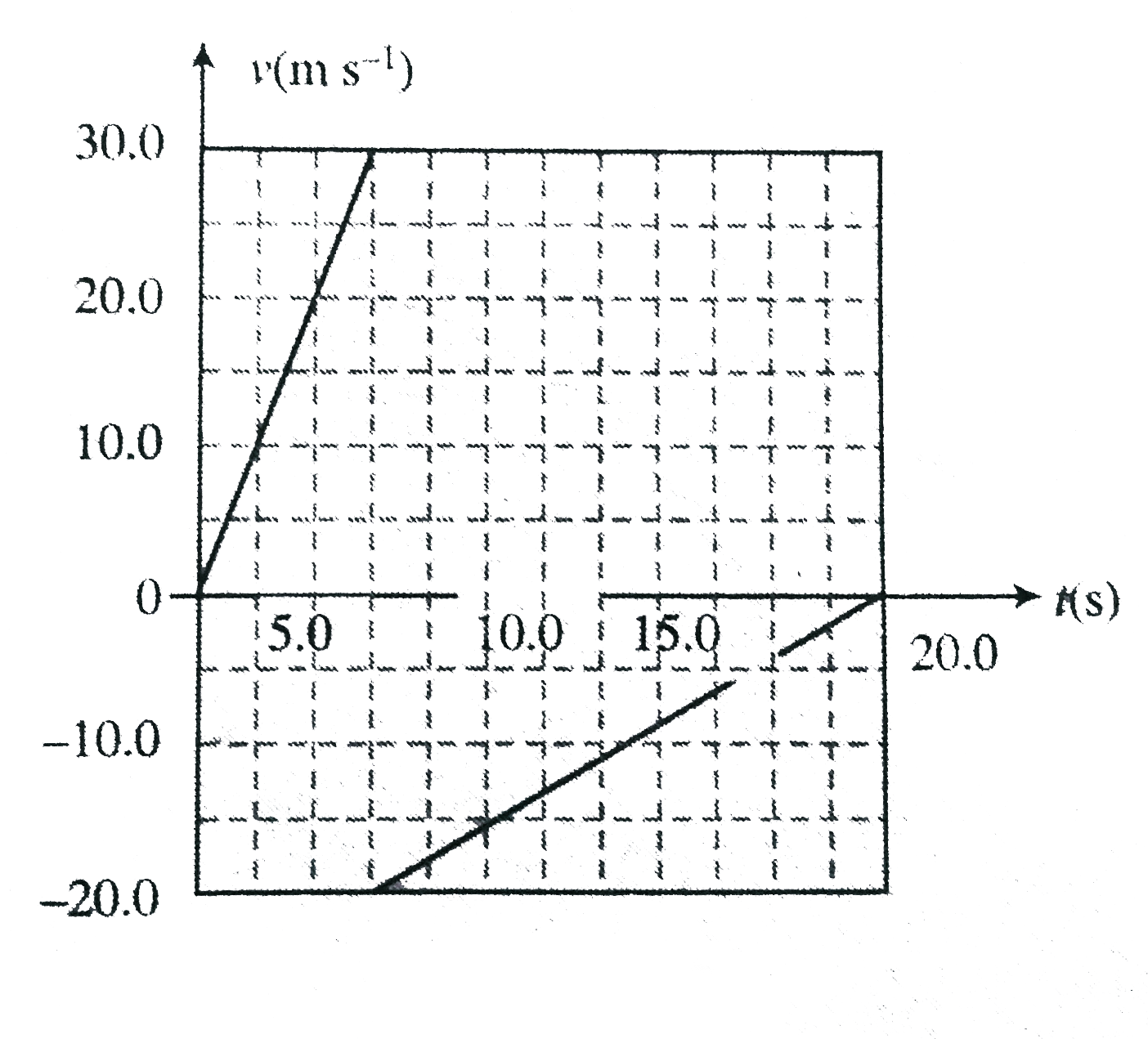
A rigid ball traveling in a straight line $thex-a\xi s$ hits a soled wall and suddenly rebounds during a brief instant . The $v_x-t$ grap in . shows this ball $s$ velocty as a function of time. During the first $20s$ of its motion, find (a) its displacement (b) the total destance the ball moves, and (c ) skerch a graph of $a_x-t$ for this ball$smotion.\left(d\right)Isthegraphshownreallyvertcalat$5 s?
Explain.
.

Explanation

For `t=0` to `5 s`,` v_(x)`, positive and the ball moves in the-x direction. The acceleration `a_(x)` is negative ball moves in the-x direction. The acceleration `a_(x)` is the slope of the `v_(x)` versus `t` graph.
a. Far `t=0` to `5 s` Displacement=Change in position
=Area under `v_(x)-t` graph
`x_(5)-x_(0)=((v_(0)_(x)+v_(x))/(2))t =(((0+3))/(2) )(5)=75 m`
The ball travels a distance of `75 m`.
For `t=5 s` to `20 s` displacement=Changein position
`x_(20)-x_(5) =((-20+0)/(2)) (15) =-150 m`
The total displacement is `x_(20)-x_(0) =55+(-150 m) =-75 m`.
The ball ends up `75 m` in the negative `x` direction from where it graph.
b. The total distance traveled is `75 m +15 m =225 m`,
c. Instantanceons acceleration is the slope of velocity-time graph.
For `t=0` to `5 s`,
`a_(x) =(30-0)/(5) =6 m s^(-2)`
For
.
`t=5 s` to `20 s`, `a_(x) =(0-(-20))/(15) =(4)/(3) m s^(-2)`
The ball of `a_(x)` versis `t` is given in .
d. The ball is in contact with the floor for a small but non-zero period of time and the direction of the velocity does change instantaneously. So, no the actul graph of `v_(x)` `t` is not really verticalcal at `5 s`.