A ball moves on a smooth floor in a straight line with a uniform velocity 10 m s−1 for 6 s. At t = 6 s, the ball hits a wall and comes back along the same line to the starting point with same speed. Draw the velocity-time graph and use it to find the total distance travelled by the ball and its displacement.
To solve the problem step-by-step, we will analyze the motion of the ball, draw the velocity-time graph, and calculate the total distance traveled and the displacement.
Step 1: Analyze the Motion of the Ball
- The ball moves with a uniform velocity of 10 m/s for 6 seconds towards the wall.
- After hitting the wall at t = 6 seconds, it returns back to the starting point with the same speed of 10 m/s.
Step 2: Calculate the Distance Traveled
- Forward Motion:
- Distance = Speed × Time
- Distance = 10 m/s × 6 s = 60 m (to the wall)
- Backward Motion:
- The ball returns to the starting point, covering the same distance of 60 m.
- Total Distance Traveled:
- Total Distance = Distance to the wall + Distance back
- Total Distance = 60 m + 60 m = 120 m
Step 3: Calculate the Displacement
- Displacement is defined as the change in position from the initial point to the final point.
- Since the ball returns to its starting point after hitting the wall, the initial and final positions are the same.
- Displacement = Final Position - Initial Position = 0 m (since both are the same)
Step 4: Draw the Velocity-Time Graph
- The graph will have time (t) on the x-axis and velocity (v) on the y-axis.
- From t = 0 to t = 6 seconds, the velocity is constant at 10 m/s (a horizontal line).
- At t = 6 seconds, the ball hits the wall and the velocity changes direction but remains the same in magnitude (10 m/s in the opposite direction).
- From t = 6 seconds to t = 12 seconds, the velocity will be -10 m/s (a horizontal line below the x-axis).
Summary of Results
- Total Distance Traveled: 120 m
- Displacement: 0 m
- The ball moves with a uniform velocity of 10 m/s for 6 seconds towards the wall.
- After hitting the wall at t = 6 seconds, it returns back to the starting point with the same speed of 10 m/s.
- Forward Motion:
- Distance = Speed × Time
- Distance = 10 m/s × 6 s = 60 m (to the wall)
- Backward Motion:
- The ball returns to the starting point, covering the same distance of 60 m.
- Total Distance = Distance to the wall + Distance back
- Total Distance = 60 m + 60 m = 120 m
- Displacement is defined as the change in position from the initial point to the final point.
- Since the ball returns to its starting point after hitting the wall, the initial and final positions are the same.
- The graph will have time (t) on the x-axis and velocity (v) on the y-axis.
- From t = 0 to t = 6 seconds, the velocity is constant at 10 m/s (a horizontal line).
- At t = 6 seconds, the ball hits the wall and the velocity changes direction but remains the same in magnitude (10 m/s in the opposite direction).
- From t = 6 seconds to t = 12 seconds, the velocity will be -10 m/s (a horizontal line below the x-axis).
- Total Distance Traveled: 120 m
- Displacement: 0 m
Topper's Solved these Questions
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (C)
Explore 3 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (C) ( Multiple choice type :)
Explore 17 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (B) ( Multiple choice type :)
Explore 3 Videos
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 2 SIMPLE PENDULUM (4 Marks Questions )
Explore 1 Video
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise -4(B)Numericals
Explore 5 Videos
Similar Questions
Draw a velocity-time graph for a body moving with an initial velocity u and uniform acceleration a. Use this graph to find the distance travelled by the body in time t.
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
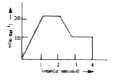
View SolutionA particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
View SolutionThe velocity-time graph of a body moving in a straight line is shown in Fig. Find the displacement and distance travelled by the body in 10 sec.
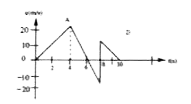
View SolutionA scooter is moving along a straight line AB covers a distance of 360 m in 24 s and returns back from B to C and coveres 240 m in 18 s. Find the total distance travelled by the scooter.
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA car travels with a uniform velocity of 20 m s−1 for 5 s. The brakes are then applied and the car is uniformly retarded. It comes to rest in further 8 s. Draw a graph of velocity against time. Use this graph to find :
(i) the distance travelled in first 5 s,
(ii) the distance travelled after the brakes are applied,
(iii) total distance travelled, and
(iv) acceleration during the first 5 s and last 8 s.
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
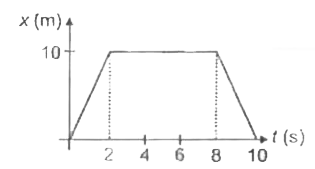
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
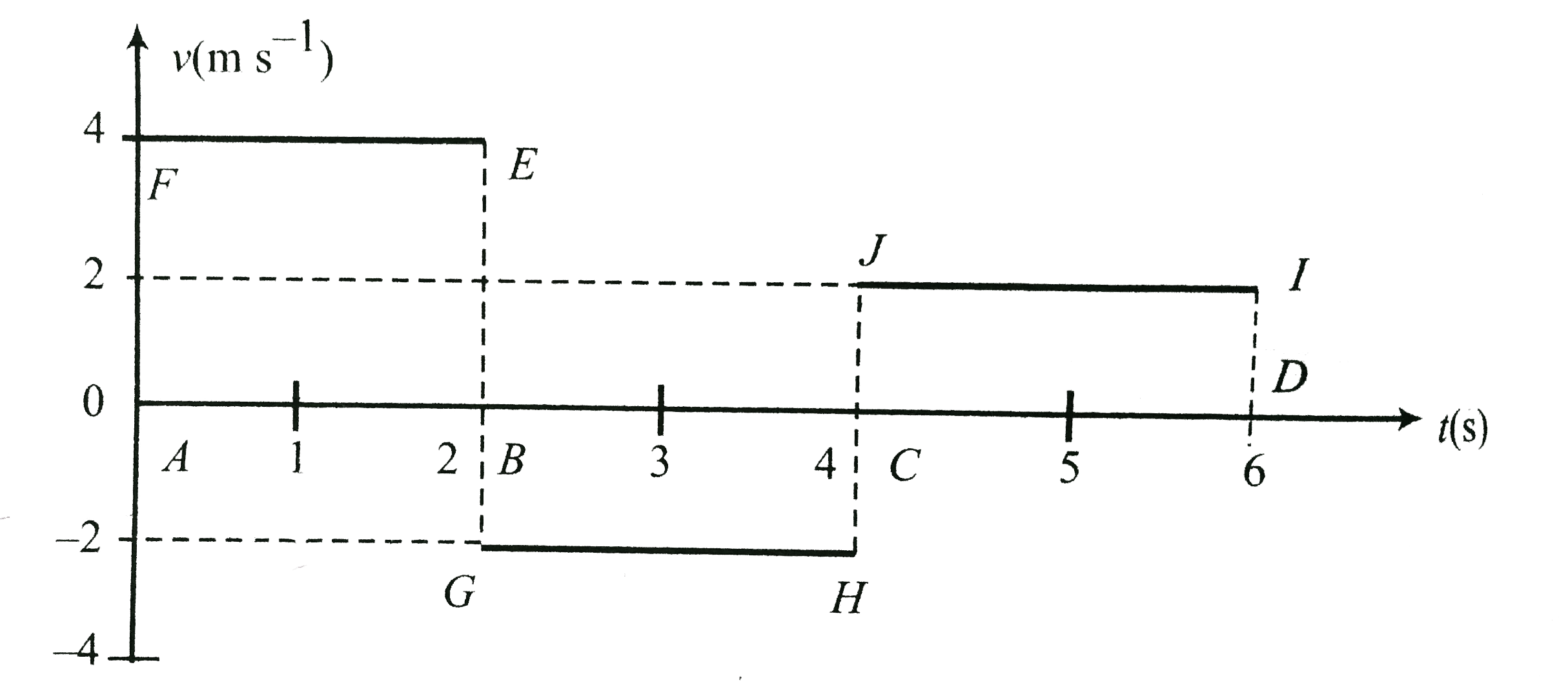 .
.
View Solution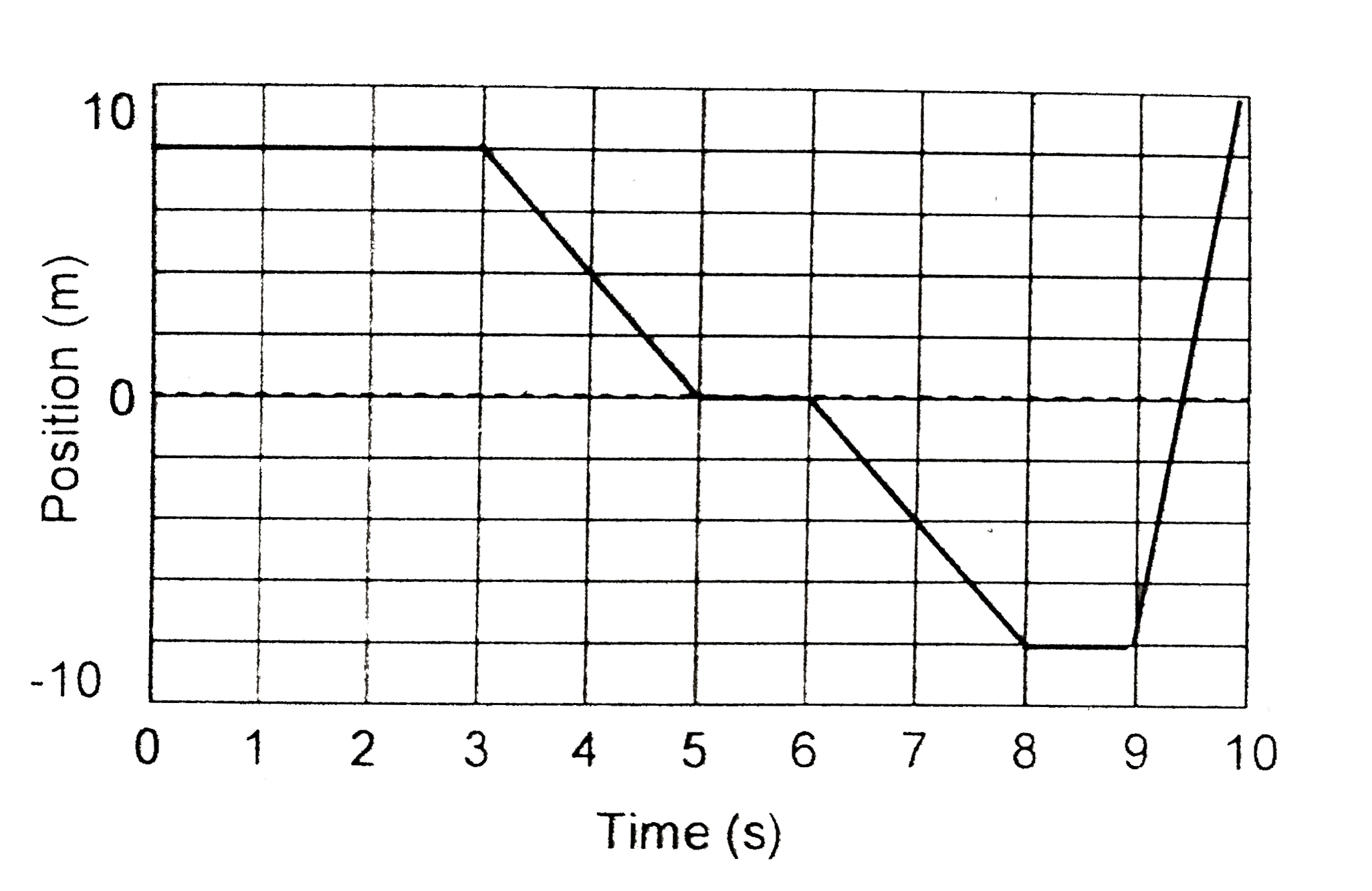
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?
View Solution

