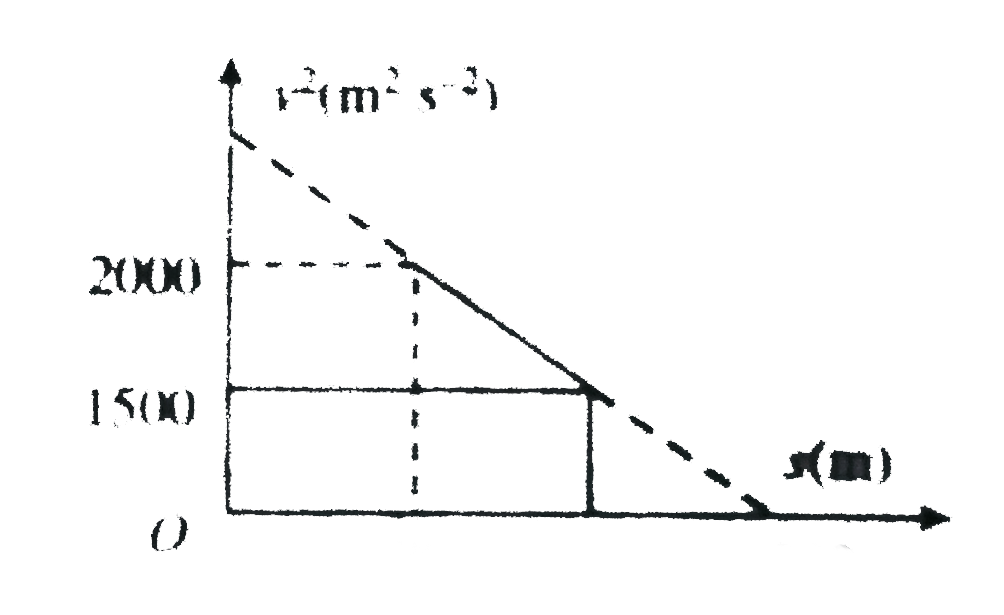
Referrring to the v2−s diagram of a particle, find the displacement of the particle durticle during the last two seconds.
 .
.
Slope of v2−s graph<br>m=-((2000-1500))/(100-50)=-10<br>Relationbetweenv_(2)ands:v^(2)=-10 s+C<br>Ats=50, v^(2)=2000<br>rArr 2000=-10xx50+C rArr C=2500<br>v=-10 s+2500<br>rArr (2v dt)/(dt)=-10(ds)/(dt)<br>rArr 2va=-10 v rArr a=-5 ms^(-2) rarrconstant<br>Tof∈d∈itialvelocity:<br>Puts=0, v=u<br>rArr u^(2)=2500 rArr u=50 ms^(-1)<br>Applyv=u+at<br>rArr 0=50-5 T<br>rArrT=10 s rarrtimeofmotion<br>Displacement during last two seconds :
S=St=10s−St=8s
=[50×10−125(10)5]−[50−125(8)2]=10m.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
velocity time graph of a particle is shown in figure. Find displacement of the particle.
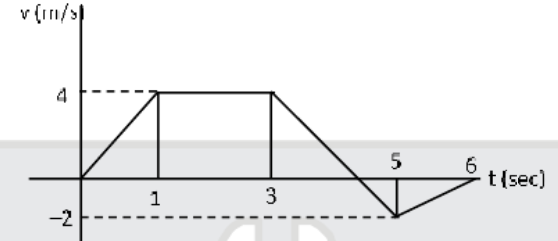
View SolutionA particle having initial velocity u moves with a constant acceleration a for a time t. a. Find the displacement of the particle in the last 1 second . b. Evaluate it for u=5m/s,a=2m/s2andt=10s.
View SolutionIf a=(3t2+2t+1) ms2 is the expression according to which the acceleration of a particle varies. Then-
Find displacement of the particle after 2 seconds of start.
View SolutionIf a=(3t2+2t+1) ms2 is the expression according to which the acceleration of a particle varies. Then-
Q. Find displacement of the particle after 2 seconds of start.
View SolutionA particle having initial velocity 4 m/s moves with a constant acceleration 1m/s2 for a time interval of 10 second in straight line. Find the displacement of the particle in the last second and the distance travelled in 10 second.
View SolutionReferring to a−s diagram as shown in , findthe velocity of the particle when the particle when the spaarticle justcovers 20m, (v0=√50ms−1.
 .
.
View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View SolutionA particle starts moving from rest such that it has uniform acceleration a0 during the 1st second of motion, uniform acceleration a02 during the 2nd second of motion, uniform acceleration a04 during the 3rd second of motion, and so on, such that it has uniform acceleration a02n−1 during the nth second of motion If the displacement of the particle during the 5th second of motion isD5=Ka032 , the value of K is
View SolutionThe v−s and v2−s graph are given for two particles. Find the accelerations of the particles at s=0.
 .
.
View SolutionA particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.
View Solution
