If the measured value of resistance R=1.05Ω, wire diameter d=0.60mm , and length l=75.3cm, then find the maximum permissible error in resistivity ,
ρ=R(πd2/4)l.
To find the maximum permissible error in resistivity, we will use the formula for resistivity given by:
ρ=R(πd24)l
Where:
- R is the resistance
- d is the diameter of the wire
- l is the length of the wire
Step 1: Identify the given values and their uncertainties
- Measured value of resistance, R=1.05Ω
- Diameter of the wire, d=0.60mm=0.60×10−3m
- Length of the wire, l=75.3cm=0.753m
Step 2: Determine the least counts (maximum permissible errors) for each measurement
- For resistance, the least count ΔR=0.01Ω
- For diameter, the least count Δd=0.01mm=0.01×10−3m
- For length, the least count Δl=0.1cm=0.001m
Step 3: Calculate the relative errors for each measurement
The formula for the maximum permissible error in resistivity can be derived from the formula for resistivity. The relative error in resistivity ρ is given by:
Δρρ=ΔRR+2⋅Δdd+Δll
Step 4: Substitute the values into the equation
1. Calculate ΔRR:
ΔRR=0.011.05
2. Calculate Δdd:
Δdd=0.01×10−30.60×10−3=0.010.60
3. Calculate Δll:
Δll=0.0010.753
Step 5: Combine the relative errors
Now, substitute these values into the equation for relative error in resistivity:
Δρρ=0.011.05+2⋅0.010.60+0.0010.753
Step 6: Calculate the numerical values
1. Calculate 0.011.05≈0.00952
2. Calculate 2⋅0.010.60≈0.03333
3. Calculate 0.0010.753≈0.00133
Now, sum these values:
Δρρ≈0.00952+0.03333+0.00133≈0.04418
Step 7: Calculate the maximum permissible error in resistivity
To find the maximum permissible error Δρ:
Δρ=ρ⋅Δρρ
First, calculate ρ:
ρ=1.05(π(0.60×10−3)24)0.753
Now, substitute this value into the equation for Δρ.
Final Answer
After calculating the above, you will have the maximum permissible error in resistivity.
---
- R is the resistance
- d is the diameter of the wire
- l is the length of the wire
- Measured value of resistance, R=1.05Ω
- Diameter of the wire, d=0.60mm=0.60×10−3m
- Length of the wire, l=75.3cm=0.753m
- For resistance, the least count ΔR=0.01Ω
- For diameter, the least count Δd=0.01mm=0.01×10−3m
- For length, the least count Δl=0.1cm=0.001m
The formula for the maximum permissible error in resistivity can be derived from the formula for resistivity. The relative error in resistivity ρ is given by:
1. Calculate ΔRR:
ΔRR=0.011.05
2. Calculate Δdd:
Δdd=0.01×10−30.60×10−3=0.010.60
Δll=0.0010.753
Now, substitute these values into the equation for relative error in resistivity:
1. Calculate 0.011.05≈0.00952
2. Calculate 2⋅0.010.60≈0.03333
3. Calculate 0.0010.753≈0.00133
To find the maximum permissible error Δρ:
After calculating the above, you will have the maximum permissible error in resistivity.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.1
16 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.2
6 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
In the experiment of Ohm's law, when potential difference of 10.0 V is applied, current measured is 1.00 A. If length of wire is found to be 10.0cm and diameter of wire 2.50 mm, then find maximum permissible percentage error in resistivity.
View SolutionThe relative error in resistivity of a material where
resistance = 1.05 + 0.01 W
diameter = 0.60 + 0.01 mm
length = 75.3 + 0.1 cm is
View SolutionThe error in the measurement of the length of the sample pendulum is 0.2% and the error in time period 4%. The maximum possible error in measurement of LT2 is
View SolutionA wire has a mass (0.3+0.003) gm, radius (0.5+0.005) mm and length (0.6+0.006) cm. The maximum percentage error in the measurement of density is
View SolutionA wire of length l=6±0.06cm and radius r=0.5±0.005cm and mass m=0.3±0.003gm. Maximum percentage error in density is
View Solution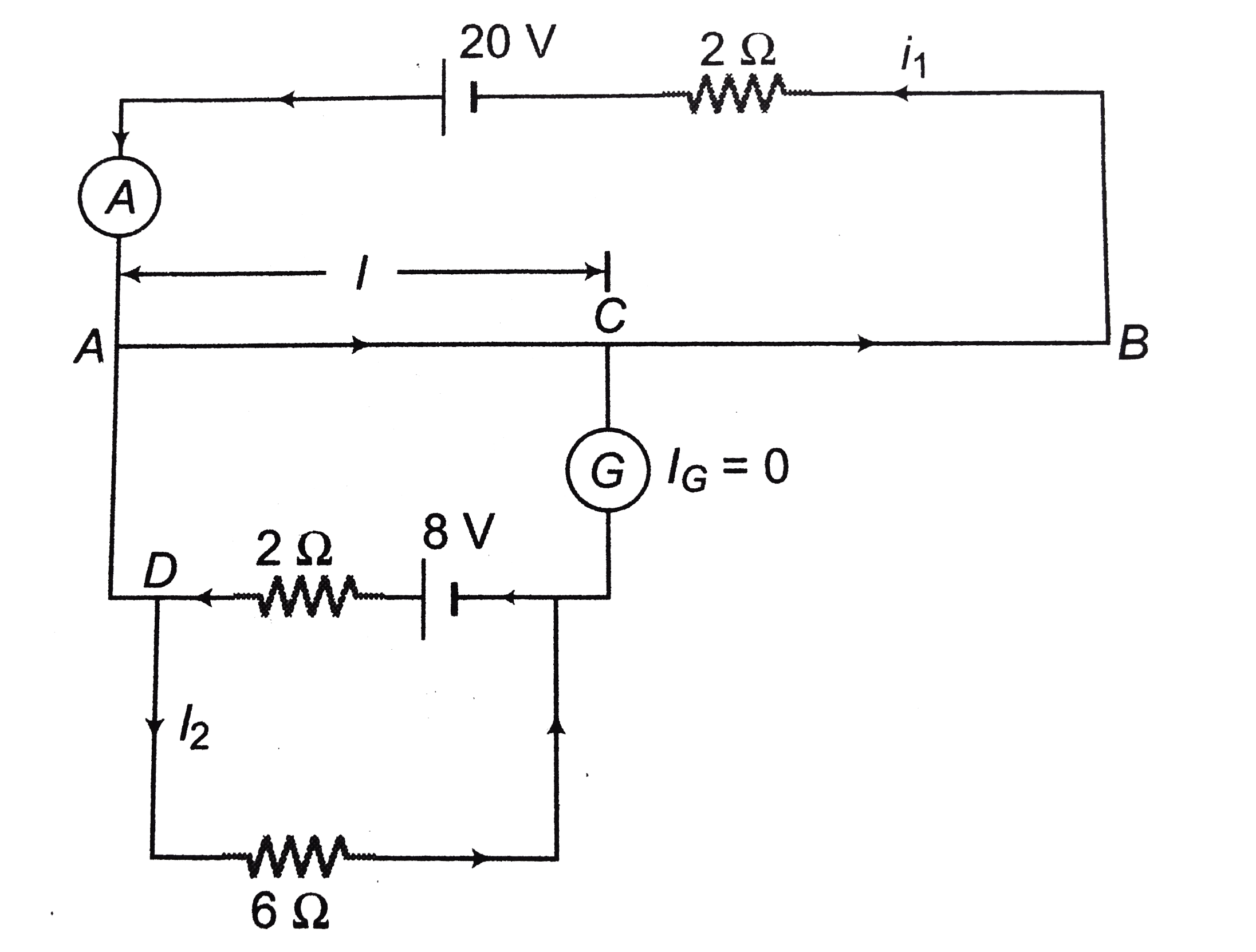
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.
View SolutionA wire has a mass (0.3±0.003)g, radius (0.5±0.005)mm and length (6±0.06)cm. The maximum percentage error in the measurement of its density is
View SolutionThe inductance L of a solenoid of length l, whose windings are made of material of density D and resistivity ρ, is (the winding resistance isR)
View SolutionIn Searle's exp to find Young's modulus, the diameter of wire is mesured as D=0.05cm length of wire is L=125cm, and when a weight, m=20.0kg is put, extension in wire was found to be 0.100cm. Find maximum permissible percentage error in Young's modulus (Y)
View SolutionIn Searl's experiment, which is used to find Young's Modulus of elasticity, the diameter of experimental wire is D=0.05cm (measured by a scale of least count 0.001cm) and length is L=110cm (measured by a scale of least count 0.1cm). A weight of 50N causes an extension of X=0.125cm (measured by a micrometer of least count 0.001cm). find the maximum possible error in the values of Young's modulus. Screw gauge and meter scale are free error.
View Solution
