Let S={(x,y)∣x,y∈R,x2+y2−10x+16=0}. The largest value of yx can be put in the form mn where m, n are relatively prime natural numbers, then m2+n2=
The correct Answer is:25
Step by step video solution for Let S={(x, y)|x,y in R, x^(2)+y^(2)-10x+16=0}. The largest value of (y)/(x) can be put in the form (m)/(n) where m, n are relatively prime natural numbers, then m^(2)+n^(2)= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBook:VK JAISWAL ENGLISHChapter:CIRCLEExercise:Exercise - 3 : Comprehension Type Problems
Explore 10 Videos
- BIONMIAL THEOREMBook:VK JAISWAL ENGLISHChapter:BIONMIAL THEOREMExercise:Exercise-4 : Subjective Type Problems
Explore 16 Videos
- COMPLEX NUMBERSBook:VK JAISWAL ENGLISHChapter:COMPLEX NUMBERSExercise:EXERCISE-5 : SUBJECTIVE TYPE PROBLEMS
Explore 8 Videos
Similar Questions
Let S={(x,y)∣x,y∈R,x2+y2−10x+16=0}. The largest value of yx can be put in the form of mn where m, n are relatively prime natural numbers, then m2+n2=
View SolutionIf the area enclosed by the curve y2=4x and 16y2=5(x−1)3 can be expressed in the form L√MN where L and N are relatively prime and M is a prime, find the value of (L+M+N).
View SolutionLet R={(x,y):x,y∈Nandx2−4xy+3y2=0}, where N is the set of all natural numbers. Then the relation R is
View SolutionIf 1m+in−x−iyx+iy=0,wherex,y,m,n are real and x+iy≠0andm+in≠0, prove that m2+n2=1.
View SolutionIf xandy are positive real numbers and m,n are any positive integers, then prove that xnym(1+x2n)(1+y2m)<14
View SolutionIf x,y∈R+and log10(2x)+log10y=2, log10x2−log10(2y)=4 and x+y=mn ,Where m and n are relative prime , the value of m−3n6 is
View SolutionLet x+1x=2,y+1y=−2 and sin−1x+cos−1y=mπ, then the value of m is
View Solutionin (M)=x
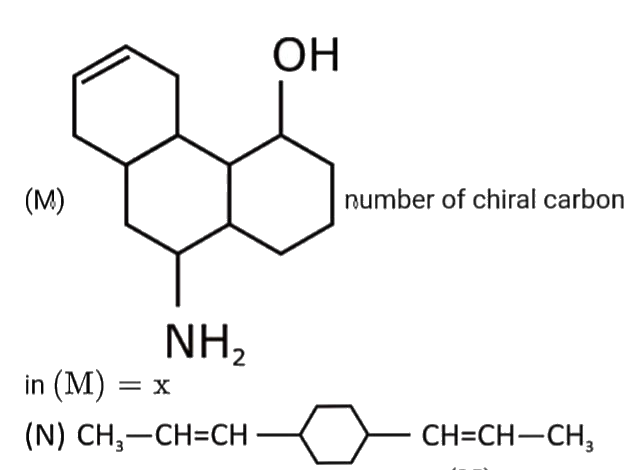
(Number of Geometrial isomers in (N)=y). The value of yx is
View SolutionSolve for x and y :
mx- ny = m2+n2
x−y=2n
View SolutionDetermine the values of m and n so that the following system of linear equations have infinite number of solutions: (2m−1)x+3y−5=0 . 3x+(n−1)y−2=0
View Solution

