If the area enclosed by the curve y2=4x and 16y2=5(x−1)3 can be expressed in the form L√MN where L and N are relatively prime and M is a prime, find the value of (L+M+N).
The correct Answer is:31
Step by step video & image solution for If the area enclosed by the curve y^(2)=4x and 16y^(2)=5(x-1)^(3) can be expressed in the form (L sqrt(M))/(N) where L and N are relatively prime and M is a prime, find the value of (L+M+N). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS - 2 EXERCISE - JEE Main (Archive)64videos
INTEGRAL CALCULUS - 2
- BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS - 2 EXERCISE - JEE Advanced (Archive)103videos
INTEGRAL CALCULUS - 2
- BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS - 2 EXERCISE - JEE Advanced (Archive)103videos
INTEGRAL CALCULUS - 2
- BOOK - VMC MODULES ENGLISHCHAPTER - FUNCTIONSEXERCISE - JEE Main & Advanced8videos
FUNCTIONS
- BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS-1EXERCISE - JEE ADVANCED (ARCHIVE)25videos
INTEGRAL CALCULUS-1
Similar Questions
If x and y vary inversely, find the values of l, m and n :
 View Solution
View SolutionIf x and y vary inversely, find the values of l, m and n :
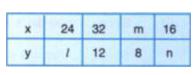 View Solution
View SolutionConsider three lines as follows. L1:5x−y+4=0 L2:3x−y+5=0 L3:x+y+8=0 If these lines enclose a triangle ABC and the sum of the squares of the tangent to the interior angles can be expressed in the form pq, where pandq are relatively prime numbers, then the value of p+q is (a)500 (b)450 (c)230 (d) 465
View SolutionConsider three lines as follows. L1:5x−y+4=0 L2:3x−y+5=0 L3:x+y+8=0 If these lines enclose a triangle ABC and the sum of the squares of the tangent to the interior angles can be expressed in the form pq, where pandq are relatively prime numbers, then the value of p+q is
View SolutionGreatest value of (sin−1x)3+(cos−1x)3ismnπ3, where m and n are relatively prime, then the value of mn is
View SolutionLet x=√3−√5andy=√3+√5 If the value of the expression x−y+2x2y+2xy2−x4y+xy4 can be expressed in the form √p+√q where p.q∈N, then find the value of (p+q).
View SolutionLet S={(x,y)∣x,y∈R,x2+y2−10x+16=0}. The largest value of yx can be put in the form of mn where m, n are relatively prime natural numbers, then m2+n2=
View SolutionFind the value of ∫+l2−l2Mlx2dx where M and l are constants .
View SolutionLet α,β,γ be the roots of x3+2x2−x−3=0. If the absolute value of the expression α−1α+2+β−1β+2+γ−1γ+2 can be expressed as mn where m and n are co-prime the value of ∣∣∣mn2m−nm+n∣∣∣ is
View Solutionlf sum of maximum and minimum value of y=log2(x4+x2+1)−log2(x4+x3+2x2+x+1) can be expressed in form ((log2m)−n), where m and n are coprime then compute (m+n).
View Solution
