Two strings (1) and (2) of equal thickness are made up of the same material. The length of the first string (1) is half that of the second string (2), while tension is (1) is twice that in the string, (2). Compare the velocities of the transverse waves on them.
The correct Answer is:V1=√T1/μ=√2T2/μ2,V2=√T2μV1:V2=√2:1(T/A)l(△/l)
To compare the velocities of the transverse waves on the two strings, we can follow these steps:
Step 1: Identify the parameters for both strings
Let:
- L1 = length of string 1
- L2 = length of string 2
- T1 = tension in string 1
- T2 = tension in string 2
- μ1 = mass per unit length of string 1
- μ2 = mass per unit length of string 2
Given:
- L1=12L2
- T1=2T2
- μ1=μ2 (since both strings are of equal thickness and made of the same material)
Step 2: Write the formula for the velocity of transverse waves
The velocity v of transverse waves on a string is given by the formula:
v=√Tμ
where T is the tension and μ is the mass per unit length.
Step 3: Calculate the velocities for both strings
For string 1:
v1=√T1μ1
For string 2:
v2=√T2μ2
Step 4: Set up the ratio of the velocities
To compare the velocities, we can set up the ratio:
v1v2=√T1/μ1√T2/μ2=√T1T2⋅√μ2μ1
Step 5: Substitute the known values
Since μ1=μ2, the ratio μ2μ1=1. Therefore, the equation simplifies to:
v1v2=√T1T2
Step 6: Substitute the tension values
We know that T1=2T2. Substituting this into the equation gives:
v1v2=√2T2T2=√2
Step 7: Conclusion
Thus, we can conclude that:
v1=√2v2
This means that the velocity of transverse waves on string 1 is √2 times the velocity on string 2.
---
Let:
- L1 = length of string 1
- L2 = length of string 2
- T1 = tension in string 1
- T2 = tension in string 2
- μ1 = mass per unit length of string 1
- μ2 = mass per unit length of string 2
- L1=12L2
- T1=2T2
- μ1=μ2 (since both strings are of equal thickness and made of the same material)
The velocity v of transverse waves on a string is given by the formula:
v=√Tμ
where T is the tension and μ is the mass per unit length.
For string 1:
v1=√T1μ1
For string 2:
v2=√T2μ2
To compare the velocities, we can set up the ratio:
v1v2=√T1/μ1√T2/μ2=√T1T2⋅√μ2μ1
Since μ1=μ2, the ratio μ2μ1=1. Therefore, the equation simplifies to:
v1v2=√T1T2
We know that T1=2T2. Substituting this into the equation gives:
v1v2=√2T2T2=√2
Thus, we can conclude that:
v1=√2v2
This means that the velocity of transverse waves on string 1 is √2 times the velocity on string 2.
Topper's Solved these Questions
- WAVESBook:ICSEChapter:WAVESExercise:From Organ Pipes
Explore 22 Videos
- WAVESBook:ICSEChapter:WAVESExercise:From Beats
Explore 15 Videos
- WAVESBook:ICSEChapter:WAVESExercise:Selected Problems (From Wave Equation, Intensity , Energy Density)
Explore 24 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:UNSOLVED PROBLEMS
Explore 79 Videos
Similar Questions
Two strings A and B of equal thickness are made of the same material. The length of A is 1/3rd that of B while tensions in A is thrice that in B. Compare the velocities of the transverse wave on them.
View SolutionTwo strings A and B, made of the same material, have equal lengths. The cross sectional area of A is half that of B while the tension on A is twice that on B. The ratio of the velocities of transverse waves in A and B is
View SolutionTwo uniform strings AandB made of steel are made to vibrate under the same tension. If the first overtone of A is equal to the second overtone of B and if the radius of A is twice that of B, the ratio of the lengths of the strings is
View SolutionThe tension in the string is changed by 2% what is the change in the transverse wave velocity
View SolutionA string of length 2L, obeying Hooke's Law, is stretched so that its extension is L. The speed of the tranverse wave travelling on the string is v. if the string is futher stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionA string of length 2L, obeying hooke's law, is stretched so that its extension is L. the speed of the transverse wave travelling on the string is v. If the string is further stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
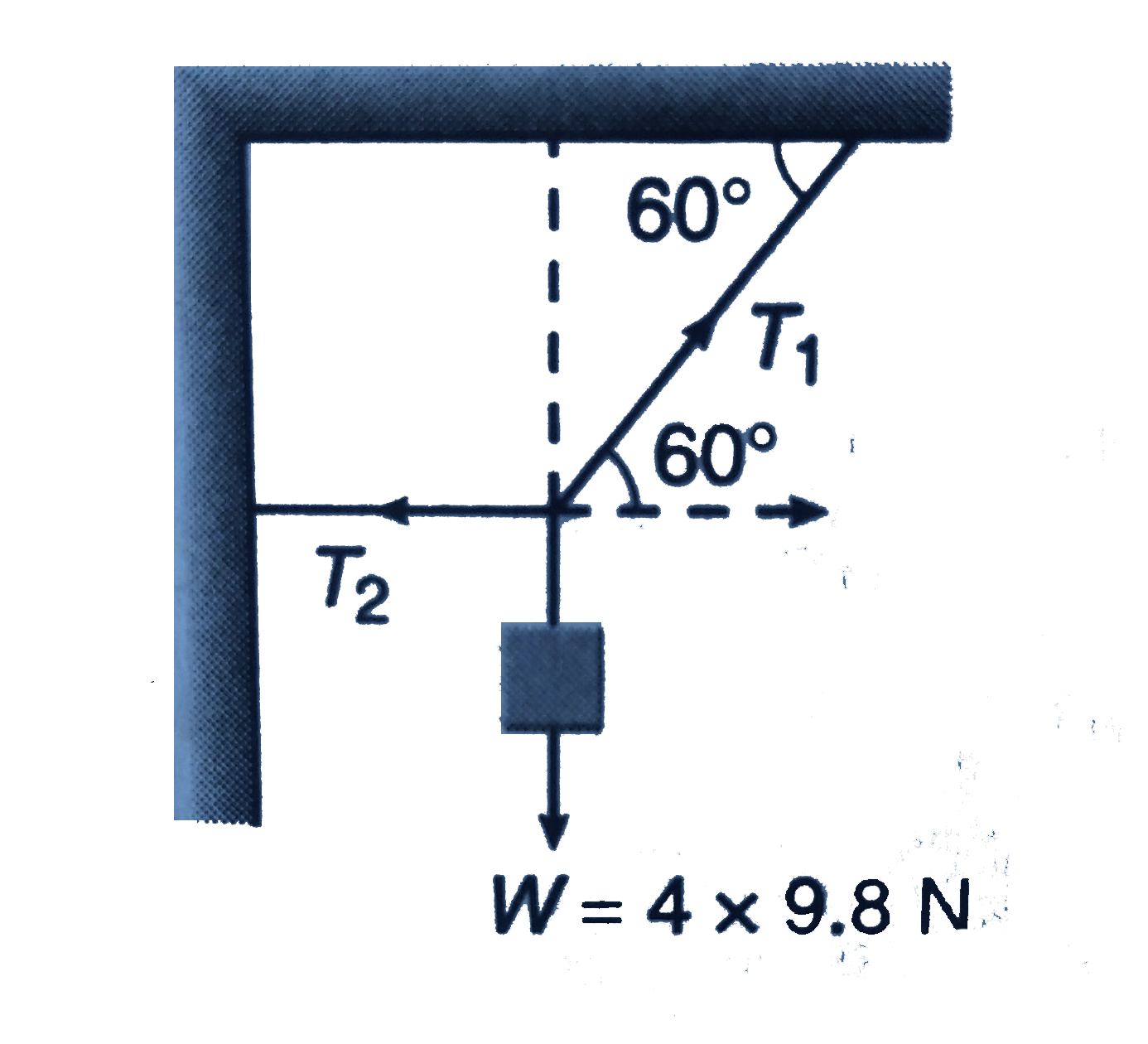
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.

View SolutionTwo strings of same material are stretched to the same tension . If their radii are in the ratio 1:2 , then respective wave velocities in them will be in ratio
View SolutionThe density of the stretched string is changed by 2% without change in tension and radius. The change in transverse wave velocity.
View Solution

