The temperateus of inside and outside of a refrigerator are 273 K and 303 K respectively. Assuming that the refrigerator cycle is reversible, for every joule of workdone, the heat delivered to the surrounding will be nearly
10 J
20 J
30 J
50 J
The correct Answer is:A
To solve the problem, we will use the principles of thermodynamics, specifically the Carnot cycle for a refrigerator. We will calculate the heat delivered to the surroundings based on the temperatures given and the work done.
1. Identify the Temperatures:
- Inside temperature (T2) = 273 K
- Outside temperature (T1) = 303 K
2. Use the Carnot Refrigerator Efficiency Formula:
The efficiency of a reversible refrigerator can be expressed as:
T2T1−T2=Q2W
where:
- Q2 = heat absorbed from the cold reservoir (inside the refrigerator)
- W = work done on the refrigerator
3. Substituting Known Values:
Since we are given that the work done W=1 Joule, we can substitute the values into the equation:
273303−273=Q21
4. Calculate the Difference in Temperatures:
T1−T2=303K−273K=30K
5. Rearranging the Equation:
Now, substituting the temperature difference:
27330=Q2
Therefore,
Q2=27330≈9.1 Joules
6. Calculate Heat Delivered to Surroundings (Q1):
We know from the first law of thermodynamics that:
Q1=W+Q2
Substituting the values:
Q1=1 Joule+9.1 Joules=10.1 Joules
7. Final Answer:
The heat delivered to the surroundings is approximately:
Q1≈10 Joules
Conclusion:
For every joule of work done, the heat delivered to the surrounding will be nearly 10 Joules.
- Inside temperature (T2) = 273 K
- Outside temperature (T1) = 303 K
The efficiency of a reversible refrigerator can be expressed as:
T2T1−T2=Q2W
where:
- Q2 = heat absorbed from the cold reservoir (inside the refrigerator)
- W = work done on the refrigerator
Since we are given that the work done W=1 Joule, we can substitute the values into the equation:
273303−273=Q21
T1−T2=303K−273K=30K
Now, substituting the temperature difference:
27330=Q2
Therefore,
Q2=27330≈9.1 Joules
We know from the first law of thermodynamics that:
Q1=W+Q2
Substituting the values:
Q1=1 Joule+9.1 Joules=10.1 Joules
The heat delivered to the surroundings is approximately:
Q1≈10 Joules
For every joule of work done, the heat delivered to the surrounding will be nearly 10 Joules.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - THERMAL CONDUCTION
17 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - THERMAL RADIATION
13 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (CALORIMETRY, CHANGE OF STATE & KINETIC THEORY OF GASES )
30 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
The temperature inside and outside a refrigerator are 273 K and 300 K respectively. Assuming that the refrigerator cycle is reversible. For every joule of work done heat delivered to the surrounding will be nearly :-
View SolutionThe temperature inside and outside of refrigator are 260K and 315K respectively . Assuming that the refrigerator cycle is reversible, calculate the heat delivered to surroundings for every joule of work done .
View Solution
Knowledge Check
The temperature inside a refrigerator is t∘2C . The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be
At1t1−t2Bt1+273t1−t2Ct2+273t1−t2Dt1+t2t1+273
A Carnot's engine works as refrigerator between 250K and 300K. It receives 500 cal heat from the reservoir at the lower temperature. The amount of work done in each cycle to operate the refrigerator is :
View SolutionThe temperature inside a refrigerator is t2 C and the room temperature is t1 C. The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be
View SolutionFour thin identical rods AB,AC,BD and EF made of the same material are joined as shown. The free-ends C,D and F are maintained at temperature T1,T2 and T3 respectively. Assuming that there is no loss of heat of the surroundings, the temperature at joint E when the steady state is attained is 1K(2T1+2T2+3T3). Find K(E is mid point of AB)
View SolutionIn a refrigerator, heat from inside at 277K is transferred to a room at 300K. How many joules of heat shall be delivered to the room for each joule of electrical energy consumed ideally?
View SolutionAn ordinary refrigerator is thermally equivalent to a box of corkboard 90 mm thick and 5.6m2 in inner surface area. When the door is closed, the inside wall is kept, on the average, 22.2∘C below the temperature of the outside wall. If the motor of the refrigerator runs 15% of the time while the door is closed, at what rate must heat be taken from the interior whicle the motor is running?
The thermal conductivity of corkboard is k=0.05W/mK.
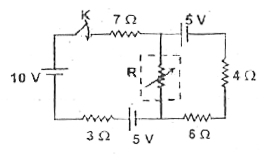
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
View SolutionA thermocol vessel contains 0.5kg of distilled water at 30∘C. A metal coil of area 5×10−3m2, number of turns 100, mass 0.06kg and resistance 1.6Ω is lying horizontally at the bottom of the vessel. A uniform time-varying magnetic field is set up to pass vertically through the coil at time t=0. The field is first increased from zero to 0.8T at a constant rate between 0 and 0.2s and then decreased to zero at the same rate between 0.2and0.4s. the cycle is repeated 12000 times. Make sketches of the current through the coil and the power dissipated in the coil as function of time for the first two cycles. Clearly indicate the magnitude of the quantities on the axes. Assumes that no heat is lost to the vessel or the surroundings. Determine the final tempreture of water under thermal equilibrium. Specific heat of metal =500jkg−1K−1 and the specific heat of water =4200jkg−1K−1. Neglect the inductance of coil.
View Solution
