The Young's modulus of brass and steel are respectively 10×1010N/m2. And 2×1010N/m2 A brass wire and a steel wire of the same length are extended by 1 mm under the same force, the radii of brass and steel wires ar RBandRSrespectively. Then
RS=√2RB
RS=RB/√2
RS=4RB
RS=RB/4
The correct Answer is:B
To solve the problem, we will use the definition of Young's modulus and the relationship between stress, strain, and the dimensions of the wires.
1. Understand Young's Modulus:
Young's modulus (Y) is defined as the ratio of stress to strain. Mathematically, it is given by:
Y=StressStrain=F/AΔL/L
where F is the applied force, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
2. Write the Expression for Each Wire:
For the brass wire:
YB=FπR2B⋅LΔL
For the steel wire:
YS=FπR2S⋅LΔL
3. Set Up the Ratio of Young's Modulus:
Since both wires are subjected to the same force and have the same original length and change in length, we can set up the ratio:
YBYS=R2SR2B
4. Substitute the Values of Young's Modulus:
Given:
- YB=10×1010N/m2
- YS=2×1010N/m2
Substitute these values into the ratio:
10×10102×1010=R2SR2B
5. Simplify the Ratio:
Simplifying the left side:
102=5⟹R2SR2B=5
6. Find the Relationship Between Radii:
Taking the square root of both sides gives:
RSRB=√5
Therefore, we can express RS in terms of RB:
RS=RB⋅√5
Final Answer:
The relationship between the radii of the brass and steel wires is:
RS=RB⋅√5
Young's modulus (Y) is defined as the ratio of stress to strain. Mathematically, it is given by:
Y=StressStrain=F/AΔL/L
where F is the applied force, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
For the brass wire:
YB=FπR2B⋅LΔL
For the steel wire:
YS=FπR2S⋅LΔL
Since both wires are subjected to the same force and have the same original length and change in length, we can set up the ratio:
YBYS=R2SR2B
Given:
- YB=10×1010N/m2
- YS=2×1010N/m2
10×10102×1010=R2SR2B
Simplifying the left side:
102=5⟹R2SR2B=5
Taking the square root of both sides gives:
RSRB=√5
Therefore, we can express RS in terms of RB:
RS=RB⋅√5
The relationship between the radii of the brass and steel wires is:
RS=RB⋅√5
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (SURFACE TENSION )
Explore 23 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (CALORIMETRY, CHANGE OF STATE & KINETIC THEORY OF GASES )
Explore 30 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:GRAVITATION
Explore 25 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
Knowledge Check
A 10 m long steel wire has mass 5 g. If the wire is under a tension of 80 N, the speed of transverse waves on the wire is
A100ms−1B200ms−1C400ms−1D500ms−1
Young.s modulus of a wire is 2×1011N/m2. If a stress of 2 x 108 N/m2 is applied at the free end of a wire, find the strain in the wire.
View SolutionThe area of cross section of a steel wire (Y=2.0×1011N/m2) is 0.1cm2. The force required to double is length will be
View SolutionThe Young's modulus of the material of a wire is 2×1010Nm−2 If the elongation strain is 1% then the energy stored in the wire per unit volume in Jm−3 is
View SolutionThe diameter of a brass rod is 4 mm and Young's modulus of brass is 9×1010N/m2. The force required to stretch by 0.1 % of its length is
View SolutionA block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
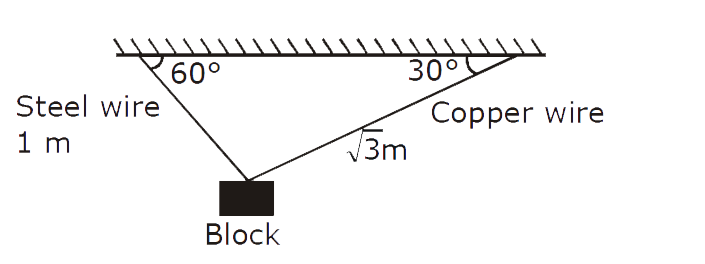
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]
View SolutionThe Young's modulus of the material of a wire is 2×1010Nm−2 If the elongation strain is 1% then the energy stored in the wire per unit volume is Jm−3 is
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View Solution

