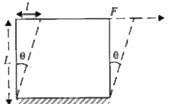
A cube of soft rubber of face area 0.02m2 whose lower face is fixed is sheared through an angle 2∘ by a force of 104N acting tangential to the upper face. Calculate the rigidity modulus of the material.
The correct Answer is:1.433×107N/m2
To solve the problem, we need to calculate the rigidity modulus (shear modulus) of the soft rubber cube using the given data. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Given Values
- Face area of the cube, A=0.02m2
- Force applied, F=104N
- Angle of shear, α=2∘
Step 2: Calculate the Shear Stress
Shear stress (τ) is defined as the force applied per unit area. The formula for shear stress is:
τ=FA
Substituting the known values:
τ=104N0.02m2=5×105N/m2
Step 3: Calculate the Shear Strain
Shear strain (γ) can be approximated by the tangent of the angle of shear. The formula is:
γ=tan(α)
Since α=2∘, we convert it to radians for calculation if necessary, but for small angles, we can use:
γ≈tan(2∘)≈0.0349(using a calculator)
Step 4: Use the Relationship Between Shear Stress, Shear Strain, and Rigidity Modulus
The relationship between shear stress, shear strain, and rigidity modulus (S) is given by:
τ=S⋅γ
Rearranging this gives:
S=τγ
Step 5: Substitute the Values to Find Rigidity Modulus
Now, substituting the values of shear stress and shear strain into the equation:
S=5×105N/m20.0349
Calculating this gives:
S≈1.43×107N/m2
Final Answer
The rigidity modulus of the material is approximately:
S≈1.43×107N/m2
---
- Face area of the cube, A=0.02m2
- Force applied, F=104N
- Angle of shear, α=2∘
Shear stress (τ) is defined as the force applied per unit area. The formula for shear stress is:
Shear strain (γ) can be approximated by the tangent of the angle of shear. The formula is:
The relationship between shear stress, shear strain, and rigidity modulus (S) is given by:
Now, substituting the values of shear stress and shear strain into the equation:
The rigidity modulus of the material is approximately:
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY) FROM WORK DONE IN STRETCHING A WIRE
4 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 2(SURFACE TENSIONS)SHORT ANSWER QUESTIONS WITH ANSWERS
14 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY) FROM BULK MODULUS
8 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
A 4 cm cube has its upper face displaced by 0.1 mm by a tangential force of 8 kN. Calculate the shear modulus of the cube.
View SolutionCalculate the pressure produced by a force of 800 N acting on an area of 2m2
View SolutionOne of the square faces of a metal slab of side 50 cm and thickness 20 cm is rigidly fixed on a horizontal surface. If a tangential force of 30 N is applied to the top face and it is known that the shear modulus of the material is 4×1010N/m2, then the displacement (in m) of the top face is
View SolutionA 0.05m cube has its upper face displaced by 0.2cm by a tangential force of 8N. Calculate the shearing strain, shearing stress and modulus of rigidity of the material of the cube.
View SolutionA steel plate of face area 4cm2 and thickness 0.5cm is fixed rigidly at the lower surface. A tangential force of 10N is applied on the upper surface. Find the lateral displacement of the upper surface with respect to the lower surface. Rigidity modulus of steel =8.4×1010Nm−2.
View SolutionA metal cube of side 20cm is subjected to a shearing force of 4000N. The top face is displaced through 0.50 cm with respect to the bottom. Find the rigidity modulus of the metal.
View SolutionA shearing force of 106 N is applied on the top surface of a fixed cube of side 10 cm. If the top surface is displaced by 0.33 mm, find rigidity modulus of the material of the cube.
View SolutionA resultant force of 45 kgf is acting on a body whose acceleration is 10 m/ sec2 . Calculate the mass of the body.
View SolutionA cube of aluminium of side 6 cm is subjected to a tangential force such that the top face is shears through 0.012cm relative to the bottom face. The tangential force is k×1010 dyne. What is the value of k? [Shear modulus of the material is η=2×1011 dyne cm−2]
View SolutionA force of 1000 N acts on an area of 0.050m2. Find the pressure in pascals.
View Solution
