If , then domain of R is
{0, 1, 2, 3, 4, 5}
{0,1,2,3,4,5,6}
{0,1,2,3,4}
{0, 1, 2, 3}
The correct Answer is:C
To find the domain of the relation R={(x,y):x,y∈W,2x+y=8}, where W represents the set of whole numbers, we will follow these steps:
Step 1: Understand the equation
The equation 2x+y=8 can be rearranged to express y in terms of x:
y=8−2x
Step 2: Determine the values of x
Since x must be a whole number (i.e., x∈W), we will substitute whole number values for x and check if y remains a whole number.
Step 3: Substitute values for x
1. For x=0:
y=8−2(0)=8(valid, as y∈W)
2. For x=1:
y=8−2(1)=6(valid)
3. For x=2:
y=8−2(2)=4(valid)
4. For x=3:
y=8−2(3)=2(valid)
5. For x=4:
y=8−2(4)=0(valid)
6. For x=5:
y=8−2(5)=−2(invalid, as y∉W)
Step 4: Identify the maximum value of x
Since y must be a whole number, we observe that for x≥5, y becomes negative. Thus, the largest value of x that keeps y in the set of whole numbers is x=4.
Step 5: List the domain
The valid whole number values for x are:
x=0,1,2,3,4
Thus, the domain of R is:
Domain of R={0,1,2,3,4}
Final Answer:
The domain of R is {0,1,2,3,4}.
---
The equation 2x+y=8 can be rearranged to express y in terms of x:
y=8−2x
Since x must be a whole number (i.e., x∈W), we will substitute whole number values for x and check if y remains a whole number.
1. For x=0:
y=8−2(0)=8(valid, as y∈W)
2. For x=1:
y=8−2(1)=6(valid)
3. For x=2:
y=8−2(2)=4(valid)
4. For x=3:
y=8−2(3)=2(valid)
5. For x=4:
y=8−2(4)=0(valid)
6. For x=5:
y=8−2(5)=−2(invalid, as y∉W)
Since y must be a whole number, we observe that for x≥5, y becomes negative. Thus, the largest value of x that keeps y in the set of whole numbers is x=4.
The valid whole number values for x are:
x=0,1,2,3,4
Thus, the domain of R is:
Domain of R={0,1,2,3,4}
The domain of R is {0,1,2,3,4}.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - RELATION AND FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)32videos
RELATION AND FUNCTIONS
- BOOK - ICSECHAPTER - QUADRATIC EQUATIONSEXERCISE - CHAPTER TEST24videos
QUADRATIC EQUATIONS
- BOOK - ICSECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2 (g)37videos
RELATIONS AND FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If R={(x,y):x,y∈N,x+2y=8} then range of R is
A{1, 2, 3, ... 7,8}B{1, 2, 3, ... 9, 10}C{1,3,5,7 ... 19}D{1,3,5,7, ... 15} - Question 2 - Select One
If R={(x,y),x,y,∈W,x2+y2≤4 then domain of R is
A{0,1,2,3}B{0,1,2}C{0,1}D{0,2,3} - Question 3 - Select One
Let A = {1,2,3,4,5,6} and R be the relation defined on A by R={(x,y):x,y∈A,x divides y}, then range of R is
A{2,3,4,5,6}B(1,2,3,4,5)C{2,4,6}D{1,2,3,4,5,6}
If R={(x,y):x,y∈W,x2+y2=25}, then find the domain and range of R.
View SolutionLet R be a relation defined on the set of natural numbers N as R={(x,y):x,y∈N,2x+y=41} Find the domain and range of R. Also, verify whether R is (i) reflexive, (ii) symmetric (iii) transitive.
View SolutionLet R be a relation defined on the set of natural numbers N as R={(x,y):x,y∈N,2x+y=41} Find the domain and range of R. Also, verify whether R is (i) reflexive, (ii) symmetric (iii) transitive.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
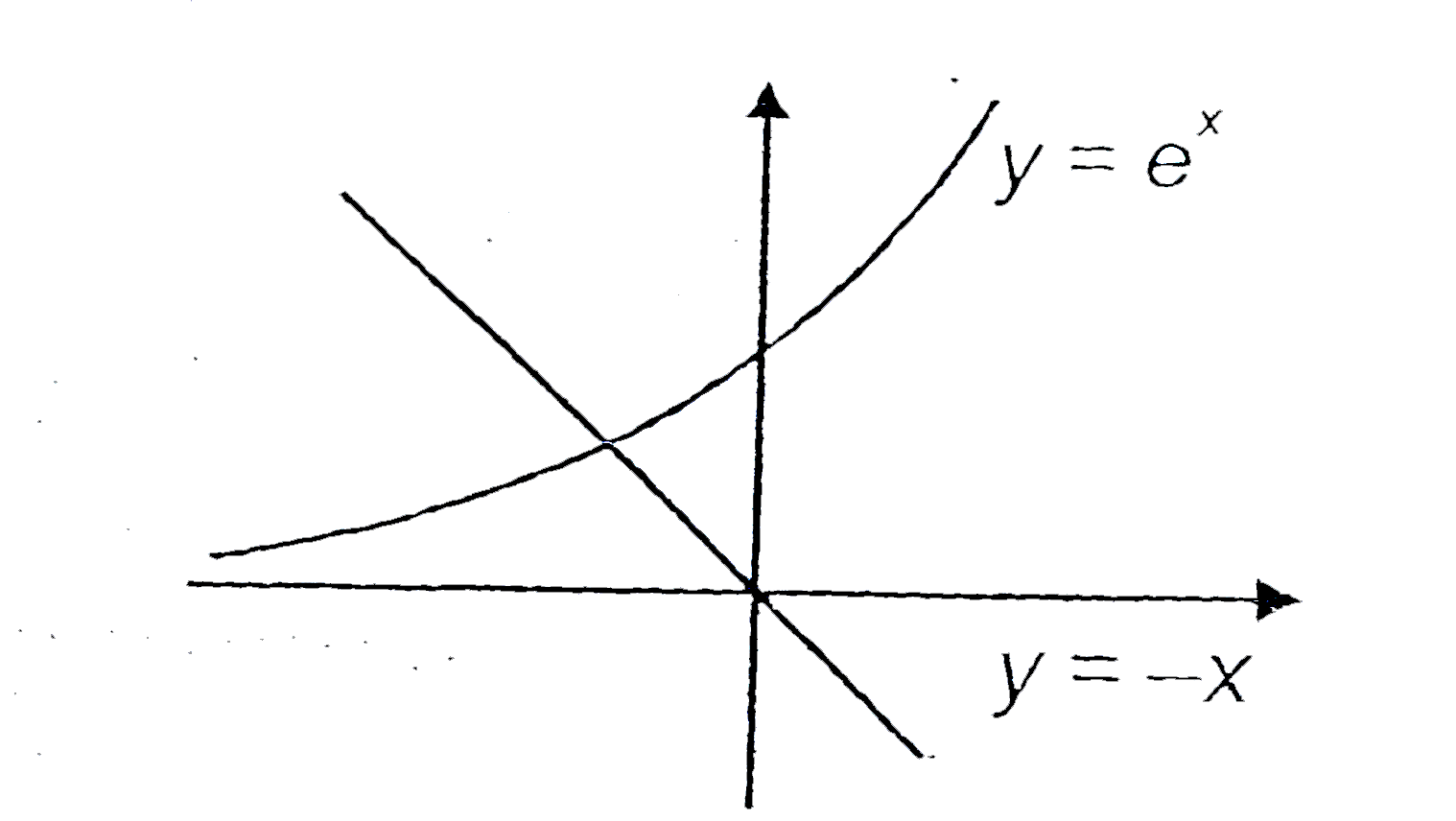
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}View SolutionGiven R={(x,y):x,y∈W,x2+y2=169}, then the domain of R is
View Solution
