Three equal charges of each are placed at the three vertices of an equilateral triangle of side 5.0cm each. Calculate the electrostatic potential energy of the system of chages.
To calculate the electrostatic potential energy of a system of three equal charges placed at the vertices of an equilateral triangle, we can follow these steps:
Step 1: Identify the charges and distances
We have three equal charges, Q1=Q2=Q3=5.0μC=5.0×10−6C. The distance between any two charges (the side of the equilateral triangle) is R=5.0cm=0.05m.
Step 2: Use the formula for interaction energy
The electrostatic potential energy U of a system of point charges is given by the formula:
U=k∑i<jQiQjrij
where k is Coulomb's constant (k=9×109N⋅m2/C2), Qi and Qj are the charges, and rij is the distance between the charges.
Step 3: Calculate the interaction energy for each pair of charges
Since we have three charges, we will consider the pairs:
1. Q1 and Q2
2. Q1 and Q3
3. Q2 and Q3
The potential energy for each pair is given by:
U12=kQ1Q2R,U13=kQ1Q3R,U23=kQ2Q3R
Step 4: Substitute the values into the formula
Since all charges are equal, we can simplify:
U12=U13=U23=kQ2R
where Q=5.0×10−6C.
Step 5: Calculate the total potential energy
The total potential energy U is the sum of the energies of the three pairs:
U=U12+U13+U23=3⋅kQ2R
Step 6: Substitute the values of k, Q, and R
U=3⋅(9×109)⋅(5.0×10−6)20.05
Calculating (5.0×10−6)2=25×10−12:
U=3⋅(9×109)⋅(25×10−12)0.05
Step 7: Simplify the expression
U=3⋅225×10−30.05=3⋅4.5×10−3=13.5J
Final Result
The electrostatic potential energy of the system of charges is:
U=13.5J
We have three equal charges, Q1=Q2=Q3=5.0μC=5.0×10−6C. The distance between any two charges (the side of the equilateral triangle) is R=5.0cm=0.05m.
The electrostatic potential energy U of a system of point charges is given by the formula:
U=k∑i<jQiQjrij
where k is Coulomb's constant (k=9×109N⋅m2/C2), Qi and Qj are the charges, and rij is the distance between the charges.
Since we have three charges, we will consider the pairs:
1. Q1 and Q2
2. Q1 and Q3
3. Q2 and Q3
U12=kQ1Q2R,U13=kQ1Q3R,U23=kQ2Q3R
Since all charges are equal, we can simplify:
U12=U13=U23=kQ2R
where Q=5.0×10−6C.
The total potential energy U is the sum of the energies of the three pairs:
U=U12+U13+U23=3⋅kQ2R
U=3⋅(9×109)⋅(5.0×10−6)20.05
Calculating (5.0×10−6)2=25×10−12:
U=3⋅(9×109)⋅(25×10−12)0.05
U=3⋅225×10−30.05=3⋅4.5×10−3=13.5J
The electrostatic potential energy of the system of charges is:
U=13.5J
Similar Questions
Knowledge Check
A point charge .q. is kept at each of the vertices of an equilateral triangle having each side .a.. Total electrostatic potential energy of the system is:
A(14πε0)3q2a2B(14πε0)3qaC(14πε0)3q2aD(14πε0)3qa2
Three charges 2 μC , -4 μC and 8 μC are places at the three vertices of an equilateral triangle of side 10 cm. The potential at the centre of triangle is
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to
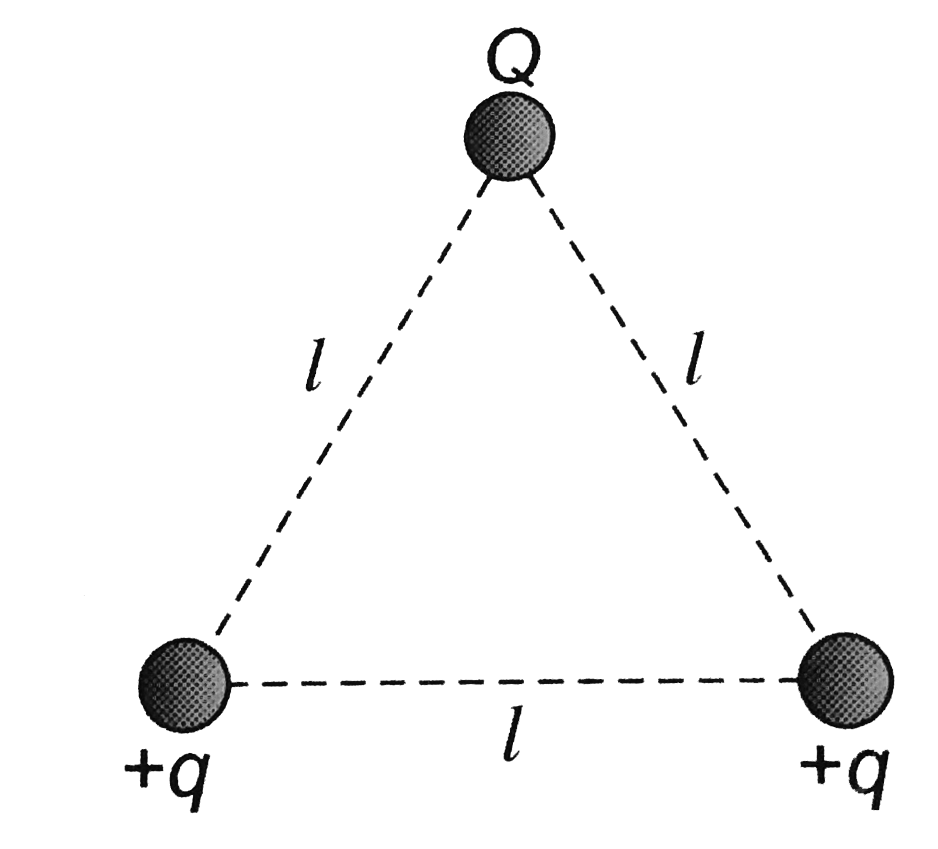
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionIf 3 charges are placed at the vertices of equilateral triangle of charge 'q' each. What is the net potential energy, if the side of equilateral Δ is lcm ?
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View Solution
