In the given figure, charge +Q is placed at the centre of a circle. Work done in taking another charge +g from A to B is W1 and from B to C is W2. What is the relation between W1=W2.
To solve the problem, we need to analyze the situation where a charge +Q is placed at the center of a circle, and we are moving another charge +q from point A to point B and then from point B to point C. We need to establish the relationship between the work done in these two movements, denoted as W1 and W2.
1. Understanding the Setup:
- Charge +Q is at the center of a circle.
- Points A, B, and C are located on the circumference of the circle.
- The distances from the center (where charge +Q is located) to points A, B, and C are equal.
2. Electric Potential Due to a Point Charge:
- The electric potential V at a distance r from a point charge Q is given by:
V=kQr
where k is Coulomb's constant.
3. Potential at Points A, B, and C:
- Since points A, B, and C are equidistant from the charge +Q (let's say the distance is r), the potential at each of these points is the same:
VA=VB=VC=kQr
4. Work Done in Moving a Charge in an Electric Field:
- The work done W in moving a charge q from one point to another in an electric field is given by:
W=q(Vf−Vi)
where Vf is the final potential and Vi is the initial potential.
5. Calculating Work Done W1 and W2:
- For the movement from A to B:
W1=q(VB−VA)=q(kQr−kQr)=q(0)=0
- For the movement from B to C:
W2=q(VC−VB)=q(kQr−kQr)=q(0)=0
6. Conclusion:
- Since both W1 and W2 are equal to zero, we can conclude that:
W1=W2=0
Final Relation:
Thus, the relation between the work done in moving the charge from A to B and from B to C is:
W1=W2
- Charge +Q is at the center of a circle.
- Points A, B, and C are located on the circumference of the circle.
- The distances from the center (where charge +Q is located) to points A, B, and C are equal.
- The electric potential V at a distance r from a point charge Q is given by:
V=kQr
where k is Coulomb's constant.
- Since points A, B, and C are equidistant from the charge +Q (let's say the distance is r), the potential at each of these points is the same:
VA=VB=VC=kQr
- The work done W in moving a charge q from one point to another in an electric field is given by:
W=q(Vf−Vi)
where Vf is the final potential and Vi is the initial potential.
- For the movement from A to B:
W1=q(VB−VA)=q(kQr−kQr)=q(0)=0
- For the movement from B to C:
W2=q(VC−VB)=q(kQr−kQr)=q(0)=0
- Since both W1 and W2 are equal to zero, we can conclude that:
W1=W2=0
Thus, the relation between the work done in moving the charge from A to B and from B to C is:
W1=W2
Similar Questions
Knowledge Check
A gas expands from i to f along the three paths indicated. The work done along the three paths denoted by W1,W2andW3 have the relationship
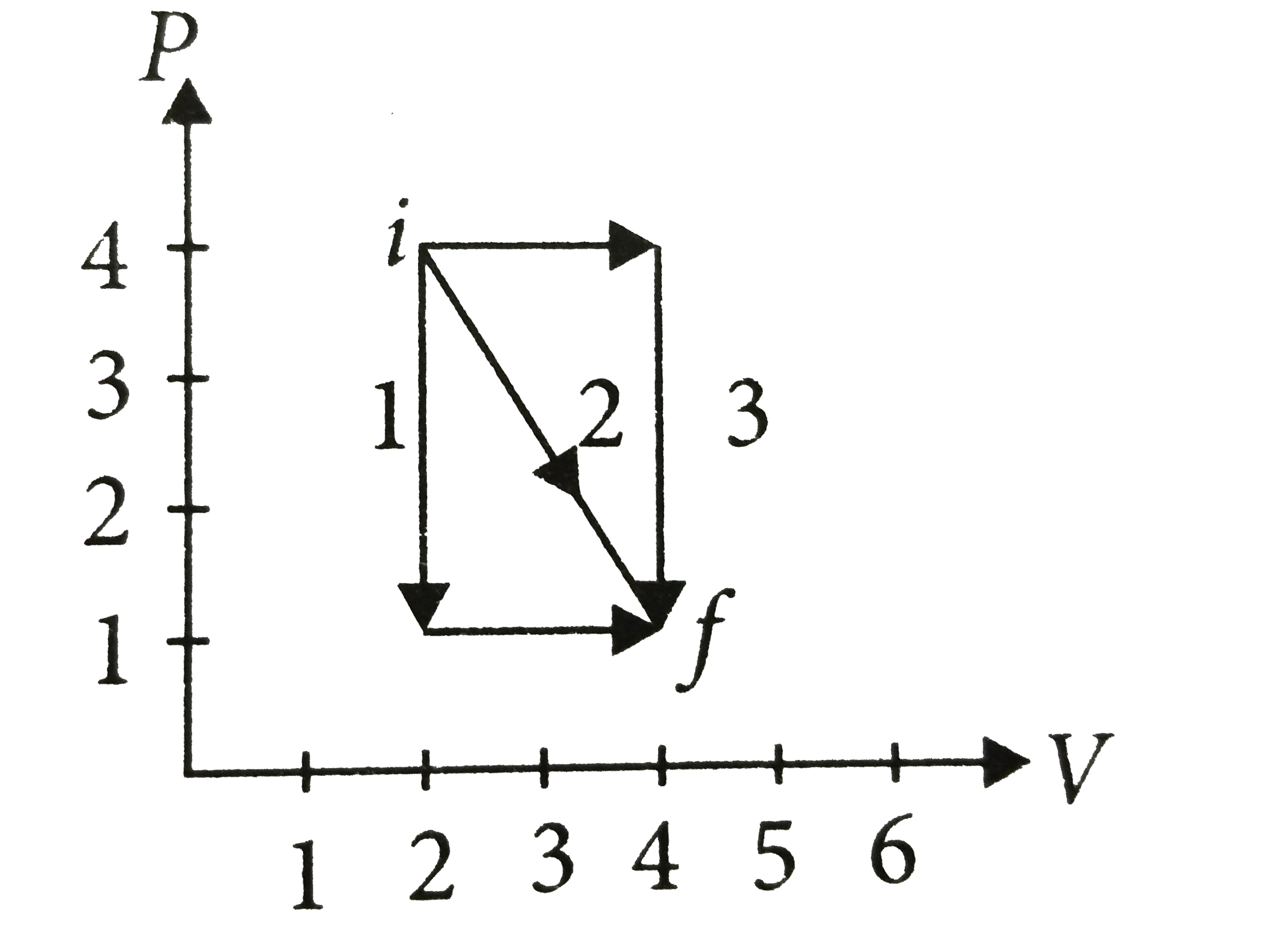 AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3
AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3
A point charge +q is placed at origin O. The work done in taking another point charge -q from the point A to point B along the circular arc as shown in the figure is
_PHY_E05_122_Q01.png) .
.
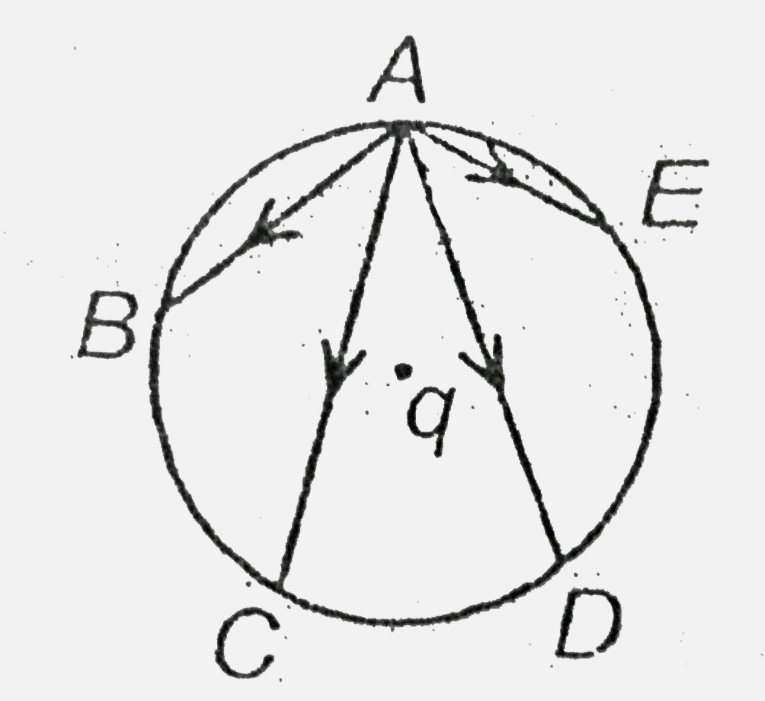
View SolutionIn the electric field of a point charge (+q) , placed at the centre of a circle , a certain test charge is carried from point A to B, C,D and E Least amount of work is done along the path
View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:
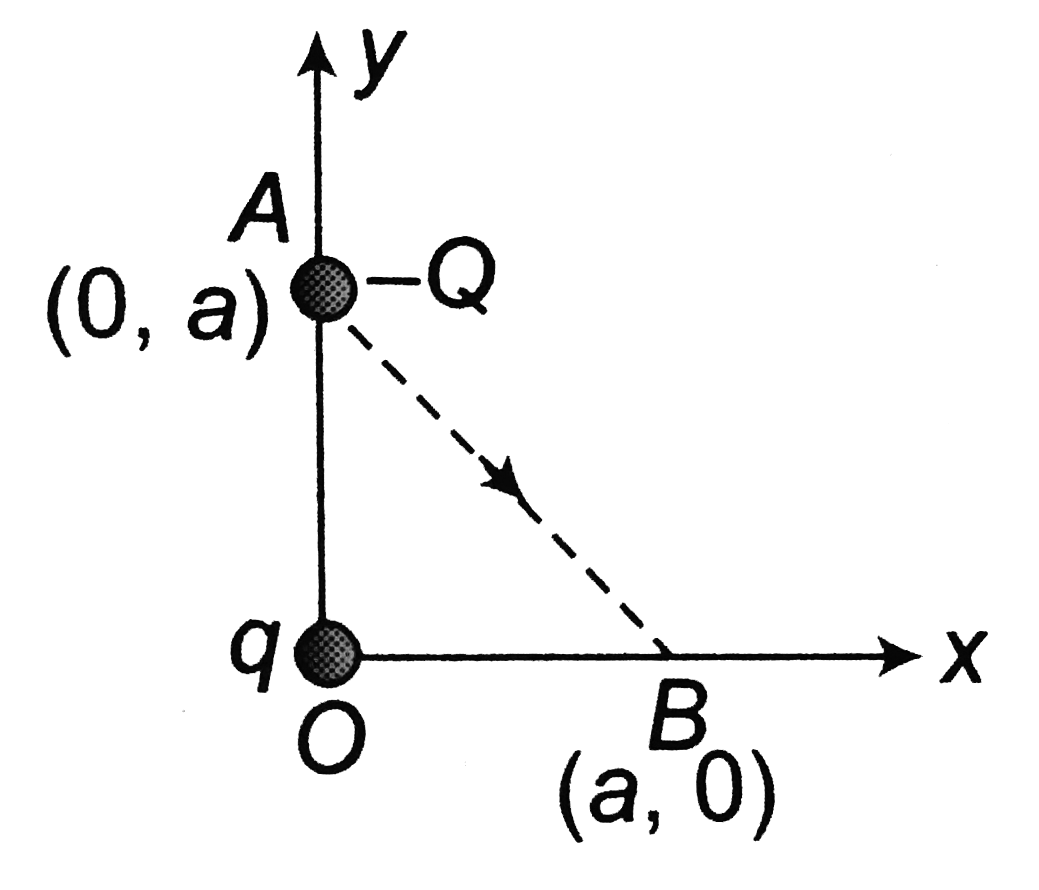
View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:

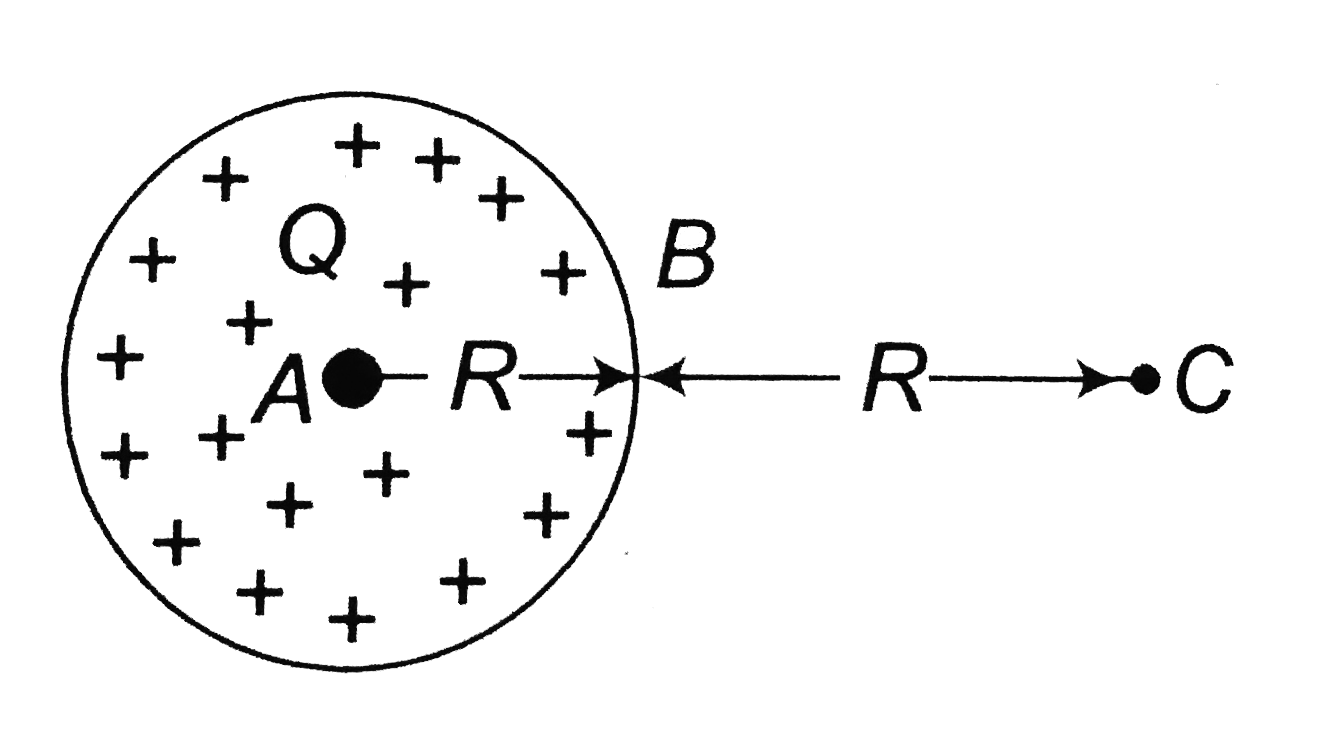
View SolutionFind the ratio of electric work done in bringing a charge q from A to B(WAB) and that from B to C(WBC) in a sphere of charge Q distributed uniformly throughout its volume.
View SolutionWork done in forming a liquid drop of radius R is W1 and that of radius 3R is W2. The ratio of work done is
View SolutionA point charge q0 is moved slowly from the centre of a ring R, ( that is carrying a charge q) to a distance x from its centre along its axis. What is the work done by the external agent in this process ?
Strategy : According to work energy theorem, if there is no change in kinetic energy, we have
Wext+WE=0
⇒Wext=−WE
=−q0(VA−VB)
View Solution


 .
.