Obtain the relation I=I0sin(ωt+π/2)andXL=1/ωC for capacitor across which an a.c. emf of e=e0 sin ot is applied as shown in the figure. Draw a phasor diagram showing emf et current I and their phase difference ϕ.
From the relation E=E0sinωt=qC,I=dqdt, then use Xc=1ωC
Similar Questions
Obtain the relation for the current I=Iosin(ωt−π/2) for a pure inductor across which an alternating emfe=eosinωt is applied.
View SolutionIf a current I given by losin(ωt−π/2) flows in an AC circuit across which an AC potential of E0.sin(ωt) has been applied, then the power consumption P in the circuit will be
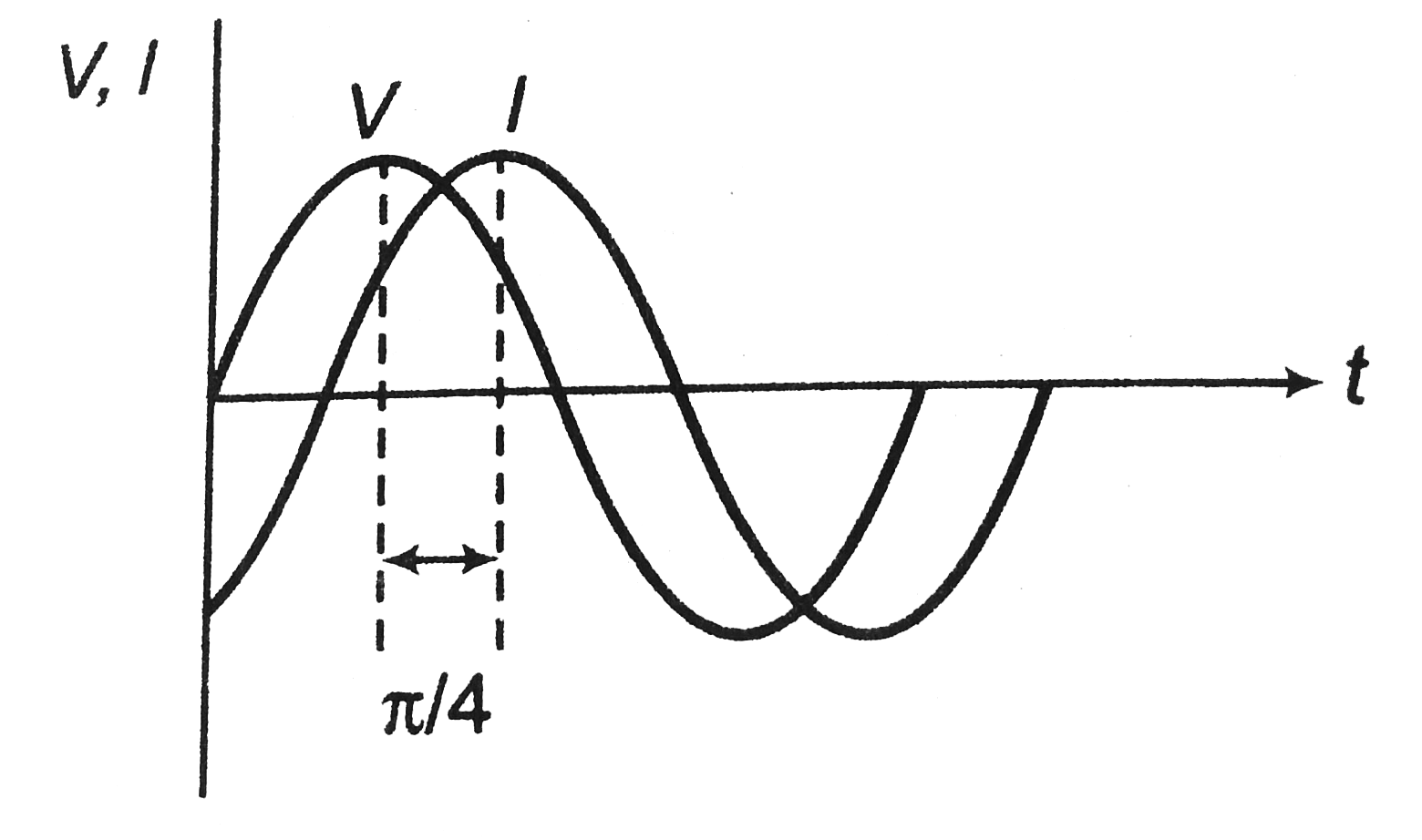
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .
.
View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .
.
View SolutionAn emf E=100sin314tV is applied across a pure capacitor of 637(μ)F. Find
(a) the instantaneous current I
(b) the instantaneous power p.
View SolutionExplain the term 'capacitive reactance'.Show graphically the variation of capacitive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied a across a pure capacitor C.Show mathematically that the current flowing through it leads the applied voltage by a phase angle of π/2
View SolutionExplain the term 'inductive reactance'.Show graphically the variation of inductive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied across a pure inductor L.Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of π/2.
View SolutionAn alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
View SolutionAn AC source producing emf V=V0 [sin ωt+sin 2ωt] is connected in series with a capacitor and a resistor. The current found in the circuit is i=i1sin 'omega' t +fi 1
View SolutionAn a.c., source of emf ε=200sinωt is connected to a resistor of 50Ω. Calculate:
Average current (Iavg)
View Solution

