The current flowing through a conductor is given by I=neAvd. (i) Identify each term in the equation. (ii) Obtain an expression for Vd, if the current flowing through the conductor of length / has its ends maintained at a potential difference V volt.
To solve the problem step by step, we will break down the equation and derive the required expression for the drift velocity Vd.
Step 1: Identify each term in the equation I=neAVd
1. Current (I): The flow of electric charge through the conductor, measured in Amperes (A).
2. n: The number of free charge carriers (electrons) per unit volume in the conductor, measured in m−3.
3. e: The charge of an electron, approximately 1.6×10−19 Coulombs (C).
4. A: The cross-sectional area of the conductor, measured in square meters (m2).
5. Vd: The drift velocity of the charge carriers, which is the average velocity of the electrons due to the electric field, measured in meters per second (m/s).
Step 2: Obtain an expression for Vd
We know that the current flowing through a conductor of length L has its ends maintained at a potential difference V. The electric field E in the conductor can be expressed as:
E=VL
The force F acting on an electron due to this electric field is given by:
F=eE
Substituting the expression for E:
F=e(VL)
Step 3: Calculate the acceleration of the electron
Using Newton's second law, the acceleration a of the electron can be expressed as:
a=Fm=e(VL)m
where m is the mass of the electron.
Step 4: Relate drift velocity to acceleration and time
The drift velocity Vd can be related to the acceleration and the time t that has elapsed since the last collision. Assuming the initial velocity is zero, we have:
Vd=at
Substituting the expression for a:
Vd=⎛⎜
⎜⎝e(VL)m⎞⎟
⎟⎠t
Step 5: Introduce relaxation time
The time t can be identified as the relaxation time τ, which is the average time between collisions of the electrons:
Vd=eVmLτ
Final Expression
Thus, the expression for the drift velocity Vd is:
Vd=eVmLτ
2. n: The number of free charge carriers (electrons) per unit volume in the conductor, measured in m−3.
3. e: The charge of an electron, approximately 1.6×10−19 Coulombs (C).
4. A: The cross-sectional area of the conductor, measured in square meters (m2).
5. Vd: The drift velocity of the charge carriers, which is the average velocity of the electrons due to the electric field, measured in meters per second (m/s).
⎜⎝e(VL)m⎞⎟
⎟⎠t
Similar Questions
When a current passes through a resistor, its temperature increases. Is it an adiabatic process?
View SolutionWrite an expression for the electrical power spent in flow of current through a conductor in terms of
resistance and potential difference
View SolutionCalculate the current flowing through a wire of resistance 5 Ω connected to a battery of potential difference 3 V.
View SolutionCalculate the current flowing through a wire of resistance 7.5 Ω connected to a battery of potential difference 1.5. V.
View SolutionA current I is flowing in a conductor of length L when it is bent in the form of a circular loop its magnetic moment
View SolutionA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)
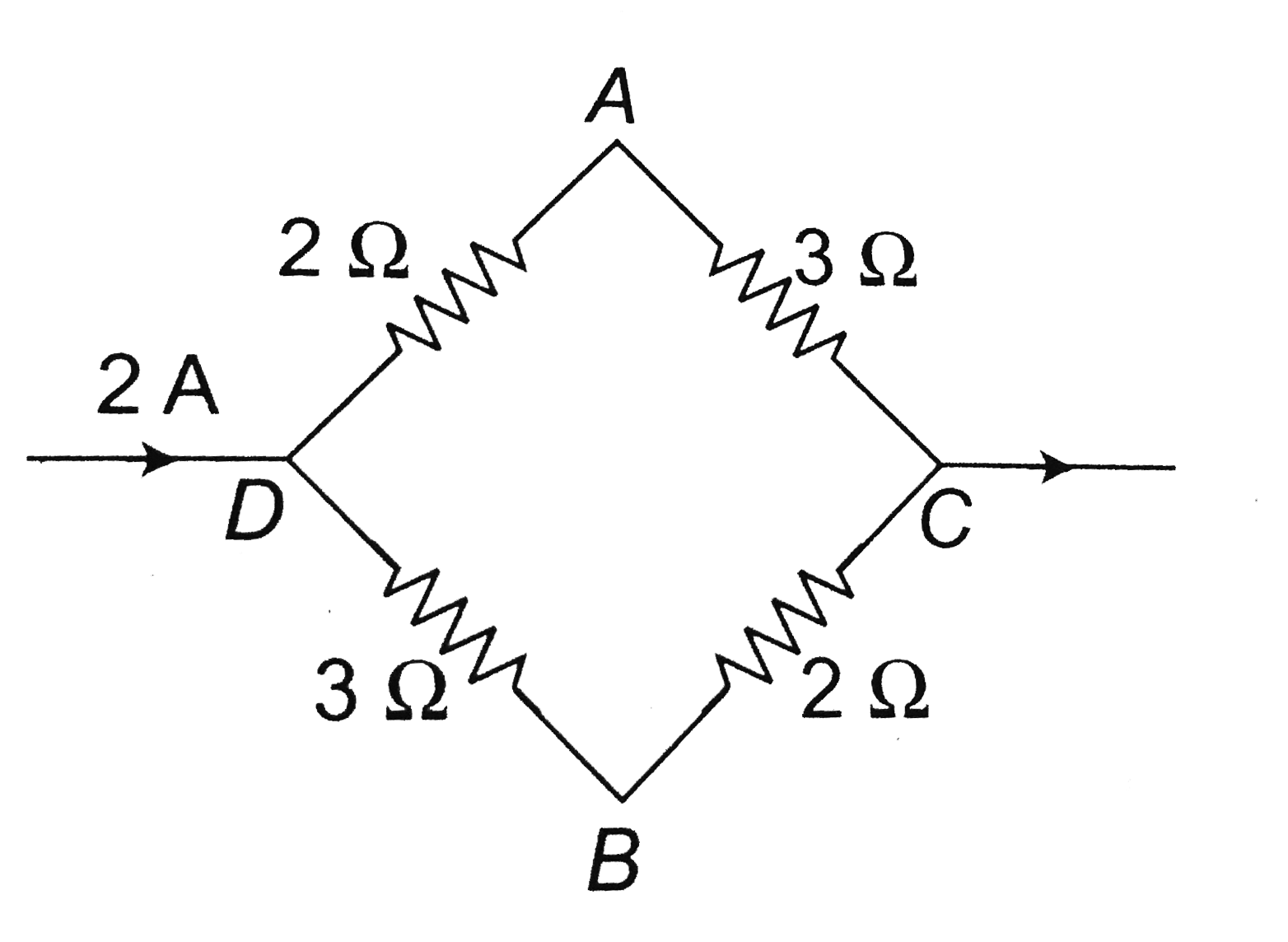
View SolutionA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)

View SolutionA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)

View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View Solution

