When a cyclist negotiates a circular path of radius .r. with velocity .v., making an angle θ with the vertical, show that tanθ=v2rg.
Motion of a cyclist on a circular path :
If a cyclist takes a turn of the road he leans towards the centre of circular path.

If the cyclist leans towards the centre of turn making an angle θ with the vertical, his weight mg and force of reaction R = mg form an anti-clockwise couple which balances the clockwise couple formed by the forces F1andF2. Thus in the position of equilibrium :
Couple formed by mg and R = Couple formed by F1andF2(=F)
mg×θsinR=F×Rcosθ
tanθ=Fmg
tanθ=mv2r×mg [F=mv2r]
tanθ=v2gr.
Topper's Solved these Questions
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - B
14 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
- SAMPLE QUESTION PAPER 4BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 4EXERCISE - SECTION - D (Answer all questions.)
7 Videos
Similar Questions
A cyclist moves around a circular path of radius 39.2√3 metre with a speed of 19.6ms−1 '. He must lean inwards at an angle θ with the vertical such that tanθ is
View Solution
A particle is moving on a circular path of radius r with uniform velocity v. The change in velocity when the particle moves from P to Q is (∠POQ=40∘)
View Solution
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
An electron is moving on a circular path of radius r with speed v in a transverse magnetic field B. e/m for it will be
View SolutionIn a conical pendulum a small mass is revolving in horizontal circle with constant speed v at the end of the cord of length L that makes an angle θ with the vertical as shown . The value of angle θ would be (where r is the radius of circle)

View SolutionA cyclist goes around a circular track of circumference 410 m in 20 s. Find the angle that his cycle makes with the vertical.
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA particle of-mass m moves along a circular path of radius r with velocity v. What is its instantaneous angular momentum about a point on the plane of the orbit at a distance x from the centre of the axis of rotation.
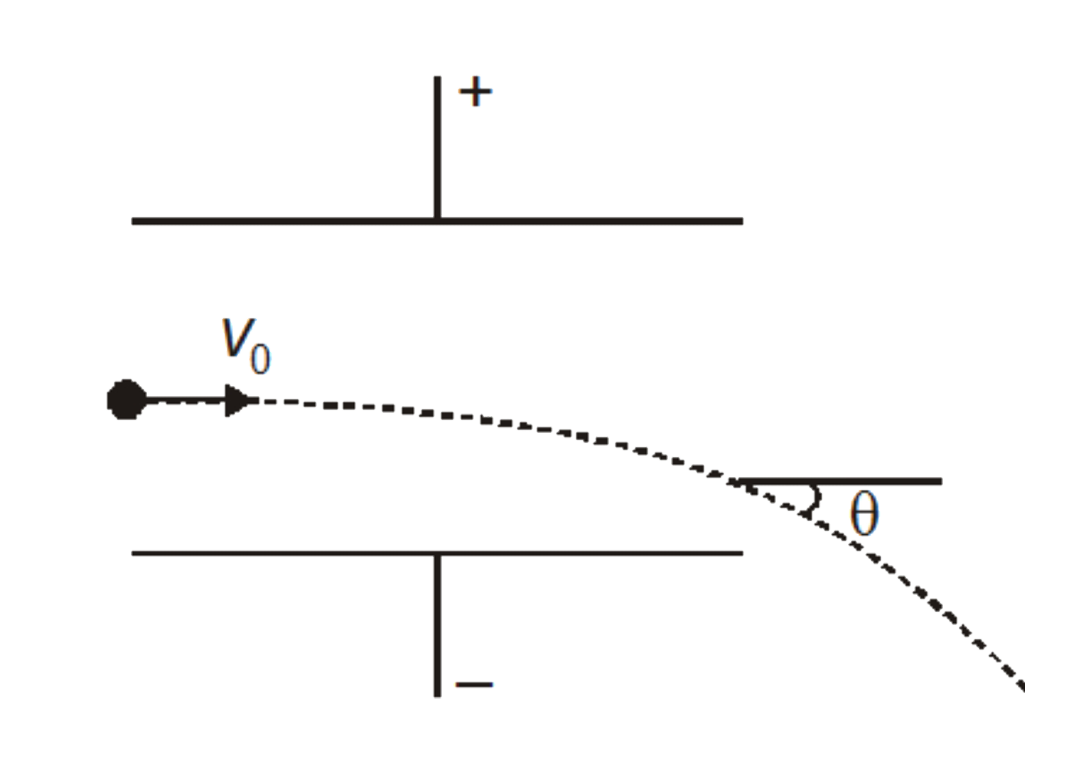
View Solutionwhen a positively charged particle is projected with a velocity v0 in the region between the horizontal plates of the capacitor then it leaves by making an angle θ with the horizontal , as shown. If θ=θ1 is for proton and θ=θ2 for an α - particle then the value of tanθ1tanθ2
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View Solution
