The value of Young.s modulus of elasticity for a perfectly rigid body is :
Zero
Infinite
1
100
The correct Answer is:B
To solve the question regarding the value of Young's modulus of elasticity for a perfectly rigid body, we can follow these steps:
1. Understanding Young's Modulus:
Young's modulus (E) is defined as the ratio of stress (σ) to strain (ε). Mathematically, it is expressed as:
E=σϵ
2. Defining Stress and Strain:
- Stress (σ) is defined as the force (F) applied per unit area (A):
σ=FA
- Strain (ε) is defined as the change in length (ΔL) divided by the original length (L₀):
ϵ=ΔLL0
3. Considering a Perfectly Rigid Body:
A perfectly rigid body is one that does not deform under any applied stress. This means that no matter how much force is applied, the length of the body does not change.
4. Calculating Strain for a Perfectly Rigid Body:
Since there is no change in length for a perfectly rigid body, the change in length (ΔL) is zero:
ΔL=0⟹ϵ=0L0=0
5. Substituting into Young's Modulus Formula:
Now, substituting the values of stress and strain into the Young's modulus formula:
E=σϵ=σ0
Since division by zero is undefined in mathematics, we can interpret this scenario as Young's modulus tending towards infinity.
6. Conclusion:
Therefore, the value of Young's modulus of elasticity for a perfectly rigid body is:
E=∞
Final Answer:
The value of Young's modulus of elasticity for a perfectly rigid body is infinity.
Young's modulus (E) is defined as the ratio of stress (σ) to strain (ε). Mathematically, it is expressed as:
E=σϵ
- Stress (σ) is defined as the force (F) applied per unit area (A):
σ=FA
- Strain (ε) is defined as the change in length (ΔL) divided by the original length (L₀):
ϵ=ΔLL0
A perfectly rigid body is one that does not deform under any applied stress. This means that no matter how much force is applied, the length of the body does not change.
Since there is no change in length for a perfectly rigid body, the change in length (ΔL) is zero:
ΔL=0⟹ϵ=0L0=0
Now, substituting the values of stress and strain into the Young's modulus formula:
E=σϵ=σ0
Since division by zero is undefined in mathematics, we can interpret this scenario as Young's modulus tending towards infinity.
Therefore, the value of Young's modulus of elasticity for a perfectly rigid body is:
E=∞
The value of Young's modulus of elasticity for a perfectly rigid body is infinity.
Topper's Solved these Questions
- SAMPLE QUESTION PAPER 4Book:ICSEChapter:SAMPLE QUESTION PAPER 4Exercise:SECTION - B (Answer all questions.)
Explore 13 Videos
- SAMPLE QUESTION PAPER 4Book:ICSEChapter:SAMPLE QUESTION PAPER 4Exercise:SECTION - C (Answer all questions.)
Explore 9 Videos
- SAMPLE QUESTION PAPER - 01 Book:ICSEChapter:SAMPLE QUESTION PAPER - 01 Exercise:SECTION - D
Explore 12 Videos
- SAMPLE QUESTION PAPER 5Book:ICSEChapter:SAMPLE QUESTION PAPER 5Exercise:SECTION - D (Answer all questions.)
Explore 6 Videos
Similar Questions
Knowledge Check
Young's modulus of a wire depends on
Adiameter of the wireBmass hanging from the wireClength of the wireDÂ material of the wire
Young's modulus of elasticity is the ratio of
View Solutionisobaric modulus of elasticity is
View SolutionAssertion The materials having low value of Young's modulus of elasticity are more ductile.
Reason If Young's modulus is less, they can be easily stretched as wires.
View Solutionwhat is the Bulk modulus for a perfect rigid body ?
View SolutionIf Young's modulus of elasticity Y for a material is one and half times its rigidity coefficient η,the Poisson's ratio σ will be
View SolutionAssertion Incompressible liquids have finite value of bulk modulus of elasticity.
Reason Compressibility is inverse of bulk modulus of elasticity.
View SolutionFor the experimental determination of Young.s modulus of elasticity Y of the material of a given wire by using Searle.s apparatus, the spherometer reading while load increasing and decreasing are tabulated below:
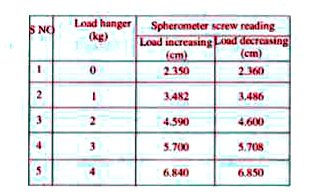
The mean extension for 2kg load is
View Solution