A firm starts producing pocket calculators. During the first year, the cost for setting up the unit is 3 lakh. The additional cost of producing a calculator is Rs 70. This cost is directly related to the production and the variable cost. The firm expects the revenue from the sales of the calculators to be 270 per calculator. Assuming all the produced calculators are sold, find the number x of the calculators for which
(i) the firm will breakeven
(ii) will make profit
(iii) will suffer a loss.
Step by step video & image solution for A firm starts producing pocket calculators. During the first year, the cost for setting up the unit is 3 lakh. The additional cost of producing a calculator is Rs 70. This cost is directly related to the production and the variable cost. The firm expects the revenue from the sales of the calculators to be 270 per calculator. Assuming all the produced calculators are sold, find the number x of the calculators for which (i) the firm will breakeven (ii) will make profit (iii) will suffer a loss. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
For manufacturing a certain item, the fixed cost is 9000 and the variable cost of producing each unit is Rs 30. The average cost of producing 60 units is -
View SolutionIt is known that cost of producing 100 units of a commodity is Rs 250 and cost of producing 200 units is Rs 300. Assuming that AVC is constant, find the cost function.
View SolutionThe cost of sales promotion per unit is
View SolutionA cycle costs Rs 8500. It cost is reduced to Rs 7990. Find the decrease per cent in its cost.
View SolutionThe cost of production of a certain instrument is directly proportional to the number of units produced. The cost of production for 300 units is $300. What is the cost of production for 270 units?
View SolutionThe marginal cost of a product is given by MC = 2x + 30 and the fixed cost is Rs. 120. Find
(i) the total cost of producing 100 units.
(ii) the cost of increasing output from 100 to 200 units.View SolutionThe cost of 213 metres of cloth is Rs 7514. Find its cost per metre.
View SolutionIf the total cost of producing x units of a commodity is given by C(x)=13x2+x2−15x+300, then the marginal cost when x=5 is
View SolutionCalculate the cost of living index number from the following group data:
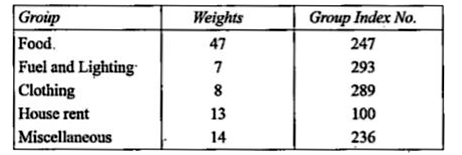 View Solution
View SolutionCalculate the cost of living index for the following data:
 View Solution
View Solution


