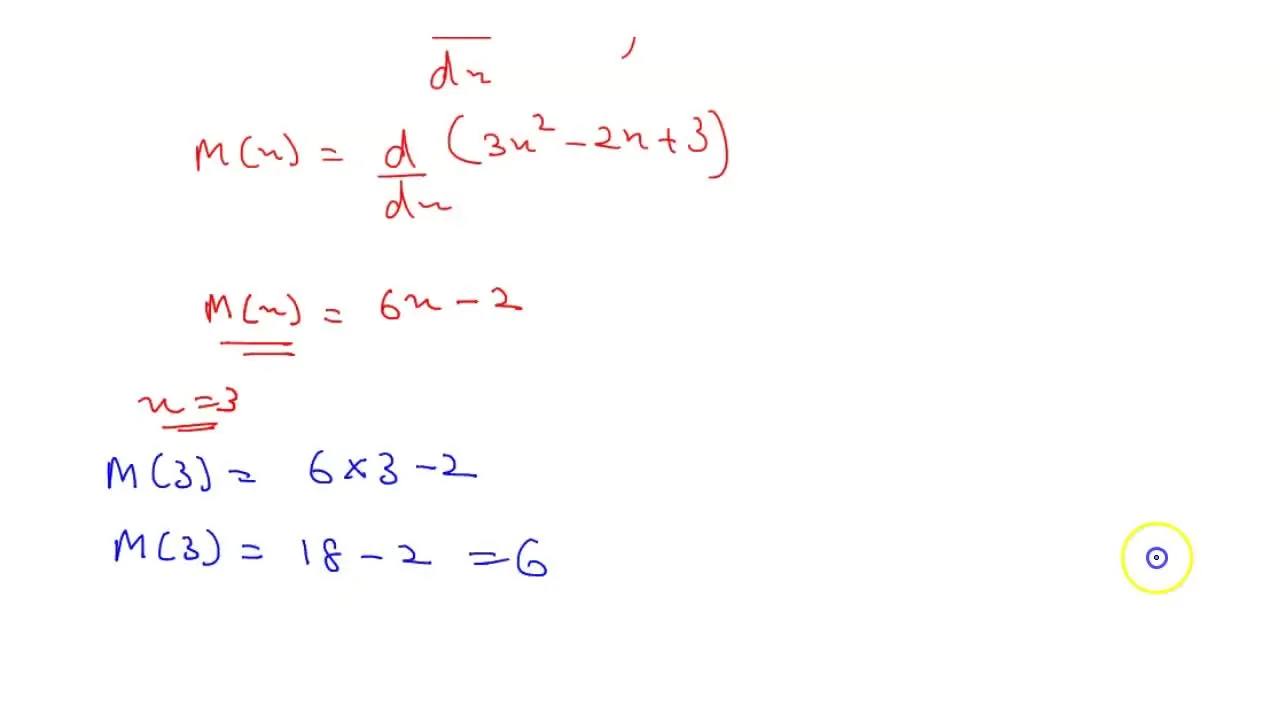If , the marginal cost when x = 3 is
24
16
11
none of the above
The correct Answer is:B
Step by step video, text & image solution for If C(x) = 3x^(2) - 2x + 3, the marginal cost when x = 3 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
If the total cost of producing x units of a commodity is given by C(x)=13x2+x2−15x+300, then the marginal cost when x=5 is
View SolutionThe total cost C(x) in rupees, associated with the production of x units of an item is given by C(x)=0.05x3−0.01x2+20x+1000. Find the marginal cost when 3 units are produced .
View SolutionIf the cost function C(x)=x3−5x2+3x+1, then find the marginal cost function.
View SolutionThe total cost C(x) in Rupees, associated with the production of x units of an item is given by C(x)=0.005x3−0.02x2+30x+5000 . Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change
View SolutionThe total cost C (x) in Rupees associated with the production of x units of an item is given by C(x)=0.007x3−0.003x2+15x+4000. Find the marginal cost when 17 units are produced.
View SolutionThe total cost C(x) in Rupees, associated with the production of x units of an item is given by C(x)=0.005x3−0.02x2+30x+5000 . Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output.
View SolutionGiven that the total cost junction for x units of a commodity is: C(x)=x33+3x2−7x+16. Find the Marginal Cost (MC) .
View SolutionGiven that the total cost function for x units of a commodity is : C(x)=x33+3x2−7x+16
(i) Find the Marginal Cost (MC) (ii) Find the Average Cost (AC)View SolutionThe total cost of daily output of x tons of coal is Rs. (110x3−3x2+50x). What is the Marginal cost funvtion .
View SolutionIf MC = 3x2+2x−1 . Determine the cost function, given that C(0) = 0
View Solution