There are two series of index numbers: P for price index and S to stock of a commodity. The mean and standard deviation of P are 100 and 8 and of S are 103 and 4 respectively. The correlation coefficient between the two series is 0.4. With these data, obtain the regression lines of P on S and S on P.
Step by step video & image solution for There are two series of index numbers: P for price index and S to stock of a commodity. The mean and standard deviation of P are 100 and 8 and of S are 103 and 4 respectively. The correlation coefficient between the two series is 0.4. With these data, obtain the regression lines of P on S and S on P. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
The mean and standard deviation of a binomial variate X are 4 and √3 respectively. Then ,P(X≥1)=
View SolutionIn the following series of reactions the major products P and S are respectively.
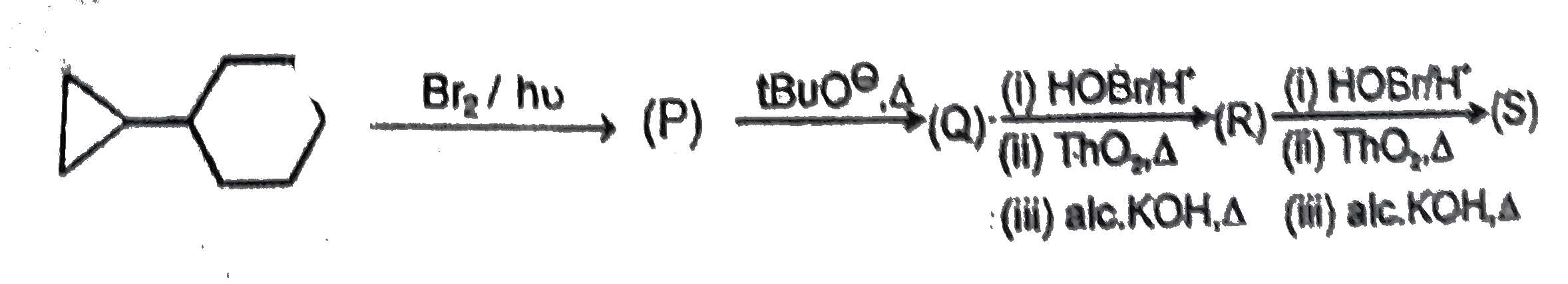 View Solution
View SolutionThe number of radial nodes in 4s and 3p orbitals are respectively
View SolutionThe distance of two points P and Q on the parabola y2=4ax from the focus S are 3 and 12 respectively. The distance of the point of intersection of the tangents at P and Q from the focus S is
View SolutionAt two point P and Q on screen in Young's double slit experiment, waves from slits S1 and S2 have a path difference of 0 and λ4 respectively. The ratio of intensities at P and Q will be:
View SolutionThe coefficient of correlation between the values denoted by X and Y is 0.5. The mean of X is 3 and that of Y is 5. Their standard deviations are 5 and 4 respectively. Find
(i) the two lines of regression.
(ii) the expected value of Y, when X is given 14
(iii) the expected value of when Y is given 9View SolutionIf ks and kp respectively are effective spring constant in series and parallel combination of springs as shown in figure, find kskp.
 View Solution
View SolutionIf coefficient of correlation between two variables X and Y is 0.64,cov(X,Y)=16 and Var(X)=9, then the standard deviation of Y series is
View SolutionThe resistance of a series combination of the resistance is S. when they are joined in parallel equvalent resistance is P. Find the value of (S2P)
View SolutionThe equivalent resistance of series combination of four equal resistors is S. If they are joined in parallel, the total resistance is P. The relation between S and P is given by S = nP. Then the minimum possible value of n is
View Solution


