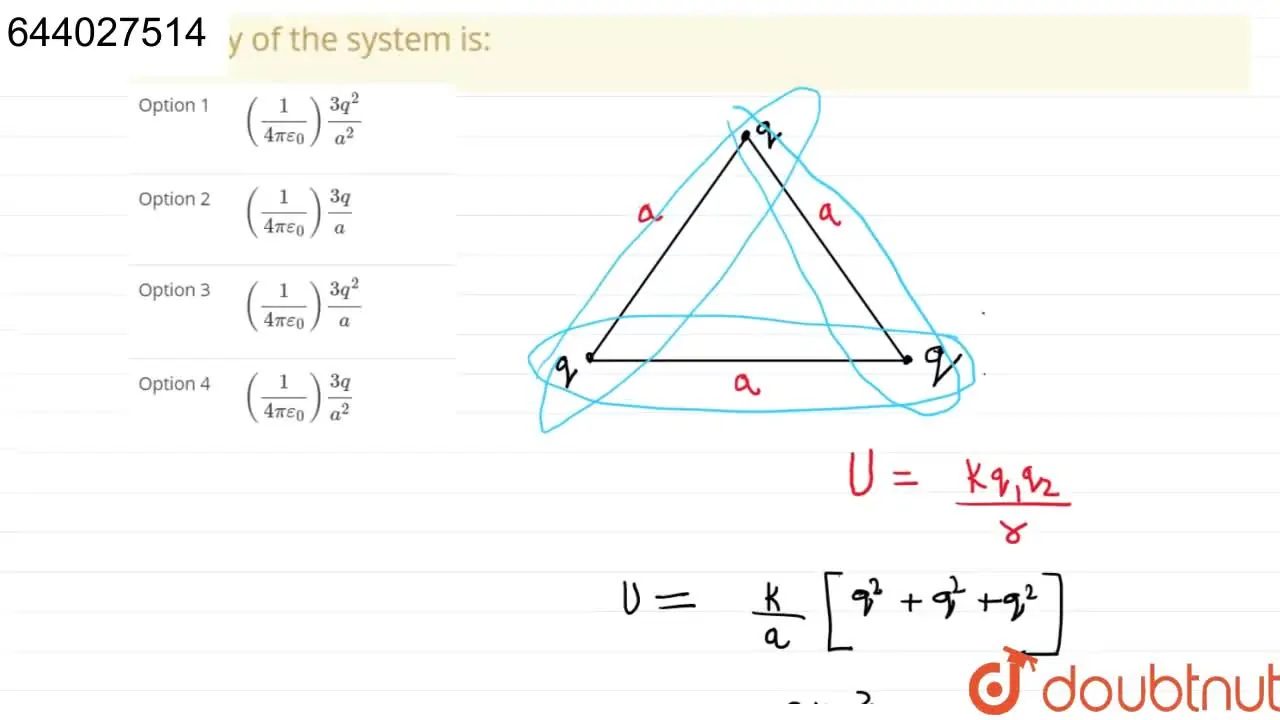
A point charge .q. is kept at each of the vertices of an equilateral triangle having each side .a.. Total electrostatic potential energy of the system is:
(14πε0)3q2a2
(14πε0)3qa
(14πε0)3q2a
(14πε0)3qa2
The correct Answer is:C
U=14πε0[q1q2r12+q1q3r13+q2q3r23]
=14πε0[q2a+q2a+q2a]
=14πε0.3q2a

Similar Questions
Choose the correct alternative (a), (b), (c) or (d) for each of the questions given below :
A point charge .q. is kept at each of the vertices of an equilateral triangle having each side .a.. Potential energy isView SolutionFind the area of an equilateral triangle having each side 4 cm.
View SolutionFind the area of an equilateral triangle having each side 4cm.
View SolutionFind the area of an equilateral triangle having each side x cm
View SolutionThree equal charges of 5.0μC each are placed at the three vertices of an equilateral triangle of side 5.0cm each. Calculate the electrostatic potential energy of the system of chages.
View SolutionThree particles, each having a charge of 10μC are placed at the coners of an equilateral triangle of side 10cm. The electrostatic potential energy of the system is (Given 14πε0=9×109N−m2/C2)
View SolutionThree point charges Q1=25μC,Q2=50μC and Q3=100μC, are kept at the corners A, B and C respectively of an equilateral triangle ABC having each side equal to 7.5 m. Calculate the total electrostatic potential energy of the system.
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to
 View Solution
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to
 View Solution
View SolutionThree charges Q0,−q and −q are placed at the vertices of an isosceles right angle triangle as in the figure. The net electrostatic potential energy is zero if Q 0 is equal to :
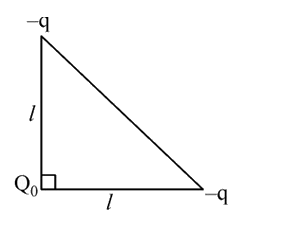 View Solution
View Solution