A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to produce product A and product B. Each unit of product A required 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs 48 per unit and product B is sold forRs 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income, Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
The correct Answer is:Rs 2320
Step by step video & image solution for A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to produce product A and product B. Each unit of product A required 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs 48 per unit and product B is sold forRs 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income, Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
, Product B and C are respectively :Knowledge Check
- Question 1 - Select One
Product (A) & (B) respectively are :A
B
C
D
Product C and D are respectively:View Solution
The product B and C are respectively:View SolutionExplain the dot product and cross product of unit vectors.
View Solution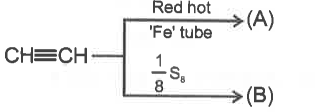
The product (A) & (B) are respectivelyView SolutionThe unit to measure productivity is
View Solution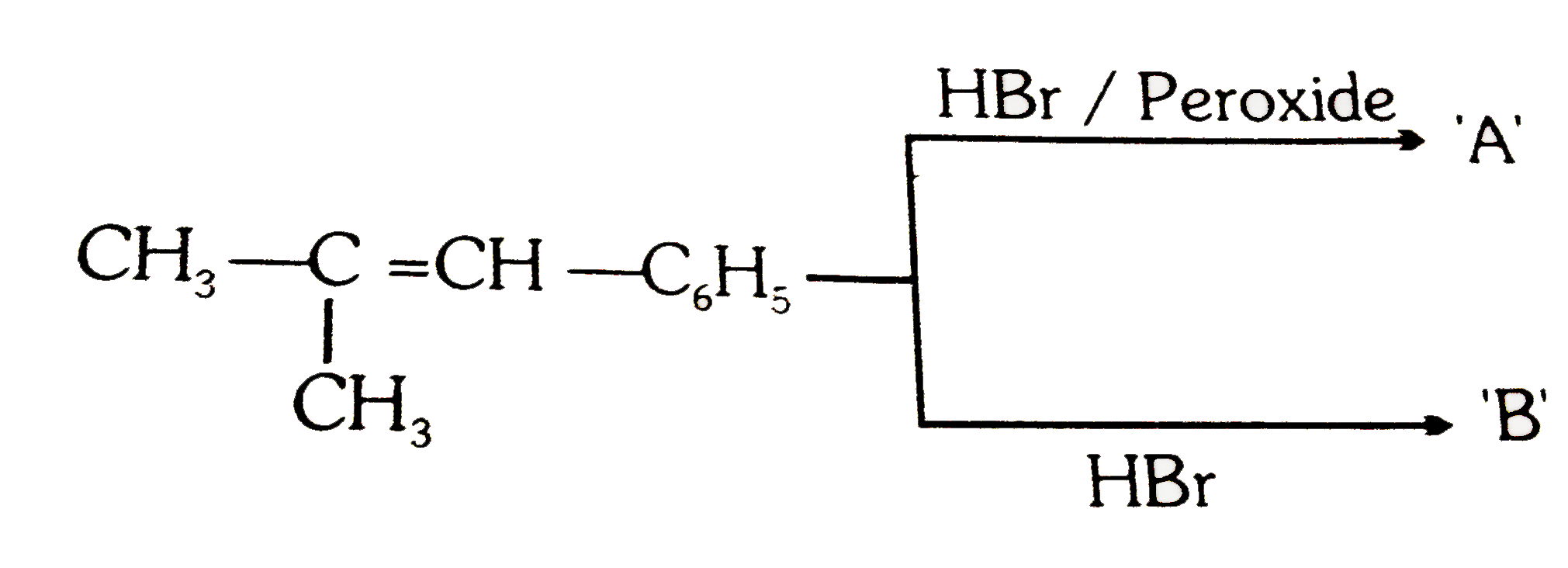
Product 'A' & 'B' are respectively-View SolutionA company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is Rs. 40 on each unit of product of type A and Rs. 50 on each unit of type B. How many units of each type should the company manufacture so as to earn maximum profit ? Use linear programming to find the solution.
View Solution