The following results were obtained with respect to two variable x and y:
∑x=30,∑y=42,∑xy=199,∑x2=184,∑y2=318,n=6.
Find the following:
(i) The regression coefficients.
(ii) Correlation coefficient between x and y.
(iii) Regression equation of y on x.
(iv) The likely value of y when x = 10.
The correct Answer is:(i) −0.458, (ii) −0.384, (iii) 0, (iv) y=5.382
To solve the problem step by step, we will follow the instructions given in the question.
Given Data:
- Σx=30
- Σy=42
- Σxy=199
- Σx2=184
- Σy2=318
- n=6
(i) Finding the Regression Coefficients
1. Calculate bxy (Regression coefficient of y on x):
bxy=nΣxy−ΣxΣynΣx2−(Σx)2
Substituting the values:
bxy=6×199−30×426×184−302
=1194−12601104−900
=−66204=−1134
2. Calculate byx (Regression coefficient of x on y):
byx=nΣxy−ΣxΣynΣy2−(Σy)2
Substituting the values:
byx=6×199−30×426×318−422
=1194−12601908−1764
=−66144=−1124
(ii) Finding the Correlation Coefficient rxy
The correlation coefficient can be calculated using the formula:
rxy=√bxy×byx
Substituting the values:
rxy=√−1134×−1124=√121816=11√816≈0.384
(iii) Regression Equation of y on x
The regression equation of y on x is given by:
y−¯y=bxy(x−¯x)
First, we need to calculate ¯x and ¯y:
¯x=Σxn=306=5
¯y=Σyn=426=7
Now substituting into the regression equation:
y−7=−1134(x−5)
Rearranging gives:
y=−1134x+5534+7
Converting 7 to a fraction:
y=−1134x+5534+23834
y=−1134x+29334
(iv) Likely Value of y when x=10
Substituting x=10 into the regression equation:
y=−1134(10)+29334
y=−11034+29334
y=293−11034=18334≈5.38
Final Answers:
1. Regression Coefficients: bxy=−1134,byx=−1124
2. Correlation Coefficient: rxy≈0.384
3. Regression Equation: y=−1134x+29334
4. Likely Value of y when x=10: y≈5.38
- Σx=30
- Σy=42
- Σxy=199
- Σx2=184
- Σy2=318
- n=6
bxy=nΣxy−ΣxΣynΣx2−(Σx)2
Substituting the values:
bxy=6×199−30×426×184−302
=1194−12601104−900
=−66204=−1134
byx=nΣxy−ΣxΣynΣy2−(Σy)2
Substituting the values:
byx=6×199−30×426×318−422
=1194−12601908−1764
=−66144=−1124
rxy=√bxy×byx
Substituting the values:
rxy=√−1134×−1124=√121816=11√816≈0.384
y−¯y=bxy(x−¯x)
First, we need to calculate ¯x and ¯y:
¯x=Σxn=306=5
¯y=Σyn=426=7
Now substituting into the regression equation:
y−7=−1134(x−5)
Rearranging gives:
y=−1134x+5534+7
Converting 7 to a fraction:
y=−1134x+5534+23834
y=−1134x+29334
y=−1134(10)+29334
y=−11034+29334
y=293−11034=18334≈5.38
1. Regression Coefficients: bxy=−1134,byx=−1124
2. Correlation Coefficient: rxy≈0.384
3. Regression Equation: y=−1134x+29334
4. Likely Value of y when x=10: y≈5.38
Topper's Solved these Questions
- MATHEMATICS-2012BOOK - ICSECHAPTER - MATHEMATICS-2012EXERCISE - SECTION-B
6 Videos
- MATHEMATICS-2012BOOK - ICSECHAPTER - MATHEMATICS-2012EXERCISE - SECTION-C
6 Videos
- MATHEMATICS-2011BOOK - ICSECHAPTER - MATHEMATICS-2011EXERCISE - SECTION-C
6 Videos
- MATHEMATICS-2015BOOK - ICSECHAPTER - MATHEMATICS-2015EXERCISE - SECTION-C
5 Videos
Similar Questions
Knowledge Check
If the regression equation of y x is given by x+ y =8 , then estimate the value of y when x is 3.5 .
A3B5.5C4.5DNone of theseThe line of regression of y on x is given by 1.63x−y=19.36 and regression equation of x on y is 0.596y−x=11.83. Estimated value of y when x= 13.5 is
A5.3B2.645C3D13.5
From the given data :

and correlation coefficient is 23. Find :
(i) Regression coefficient byxandbxy
(ii) Regression line x on y.
(iii) Most likely value of x when y=14.
View SolutionFind the regression equation of y on x on the basis of following data.

View Solution2x+3y−5=0 is the regression equation of x on y. Find its slope
View SolutionYou are given the following data:
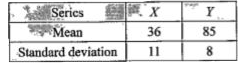
Correlation coefficient between x and y=0.66. Find the equations of the lines of regression.
View SolutionFind the Karl Pearson's coefficient of correlation between X and Y for the following data :

View SolutionIn a blvariate data ∑x=30,∑y=400,∑x2=196,∑xy=850andn=10. Find the regression coefficient of y on x.
View Solution
