From the given data : 
and correlation coefficient is 23. Find :
(i) Regression coefficient byxandbxy
(ii) Regression line x on y.
(iii) Most likely value of x when y=14.
The correct Answer is:8.67
Step by step video, text & image solution for From the given data : and correlation coefficient is 2/3. Find : (i) Regression coefficient b_(yx) and b_(xy) (ii) Regression line x on y. (iii) Most likely value of x when y=14. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION PAPER-2018BOOK - ICSECHAPTER - QUESTION PAPER-2018EXERCISE - Section -B
8 Videos
- QUESTION PAPER 2022 TERM 1BOOK - ICSECHAPTER - QUESTION PAPER 2022 TERM 1EXERCISE - SECTION C
8 Videos
- RELATIONS AND FUNCTIONS BOOK - ICSECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - MULTIPLE CHOICE QUESTIONS (Competency based questions)
20 Videos
Similar Questions
The following results were obtained with respect to two variable x and y:
∑x=30,∑y=42,∑xy=199,∑x2=184,∑y2=318,n=6.
Find the following:
(i) The regression coefficients.
(ii) Correlation coefficient between x and y.
(iii) Regression equation of y on x.
(iv) The likely value of y when x = 10.
View SolutionFrom the following data, find (i) regression coefficients (ii) regression equations
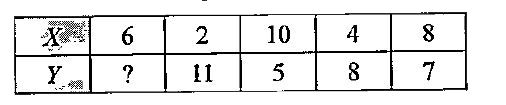
View Solution
Knowledge Check
Given regression co-efficient of y on x is 0.4 and r(x,y) = 2√10 , then the regression co-efficient of x on y is
A1B0.2C√10D2
From the following data, find () regression coefficients (ii) regression equations.

View SolutionFind the regression coefficient byxandbxy when the lines of regression are
6x−5y+10=0,10x−3y−28=0.
View SolutionFor the given lines of regression, 3x – 2y = 5 and x - 4y - 7, find
regression coefficients byx and bxy
View SolutionRegression equation of Y on X 2x+3y-12=0. The value of byx is
View SolutionIf the regression coefficients be given by byx=29 and bxy=2 and θ be angle between the regression lines find the value of theta.
View SolutionIf the regression coefficients be given byx=1.6andbxy=0.4 then find the sum of the slopes of the two regression lines.
View SolutionWrite the coefficient of:
(i)y in −3y
(ii) a in 2ab
View Solution
