ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
PQ:DB is equal to
23
13
12
34
The correct Answer is:B
∴PQ=12DB,
i.e., PQ:DB=1:2
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHS ENGLISHChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHS ENGLISHChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHS ENGLISHChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratio
View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P. M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratio
View SolutionIn ΔABC, a point P on BC divided BC in the ratio 1:1. what is the line segment joining vertex A and P called ?
View SolutionABCD is parallelogram. If LandM are the middle points of BC and CD, then ¯¯¯¯¯¯AL+¯¯¯¯¯¯¯AM equals
View SolutionABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2
Calculate
The ratio of PA : DC.
View SolutionThe origin O,B (-6,9) and C (12, -3) are vertices of triangle OBC, Point P divides OB in the ratio 1 : 2 and point Q divides OC in the ratio 1 : 2 Find the co-ordinates of points P and Q. Also show that PQ=13 BC.
View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC and AE intersects CD at F.
If ar.(ΔDFB)=30cm2, find the area of parallelogram
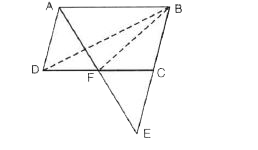
View SolutionABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
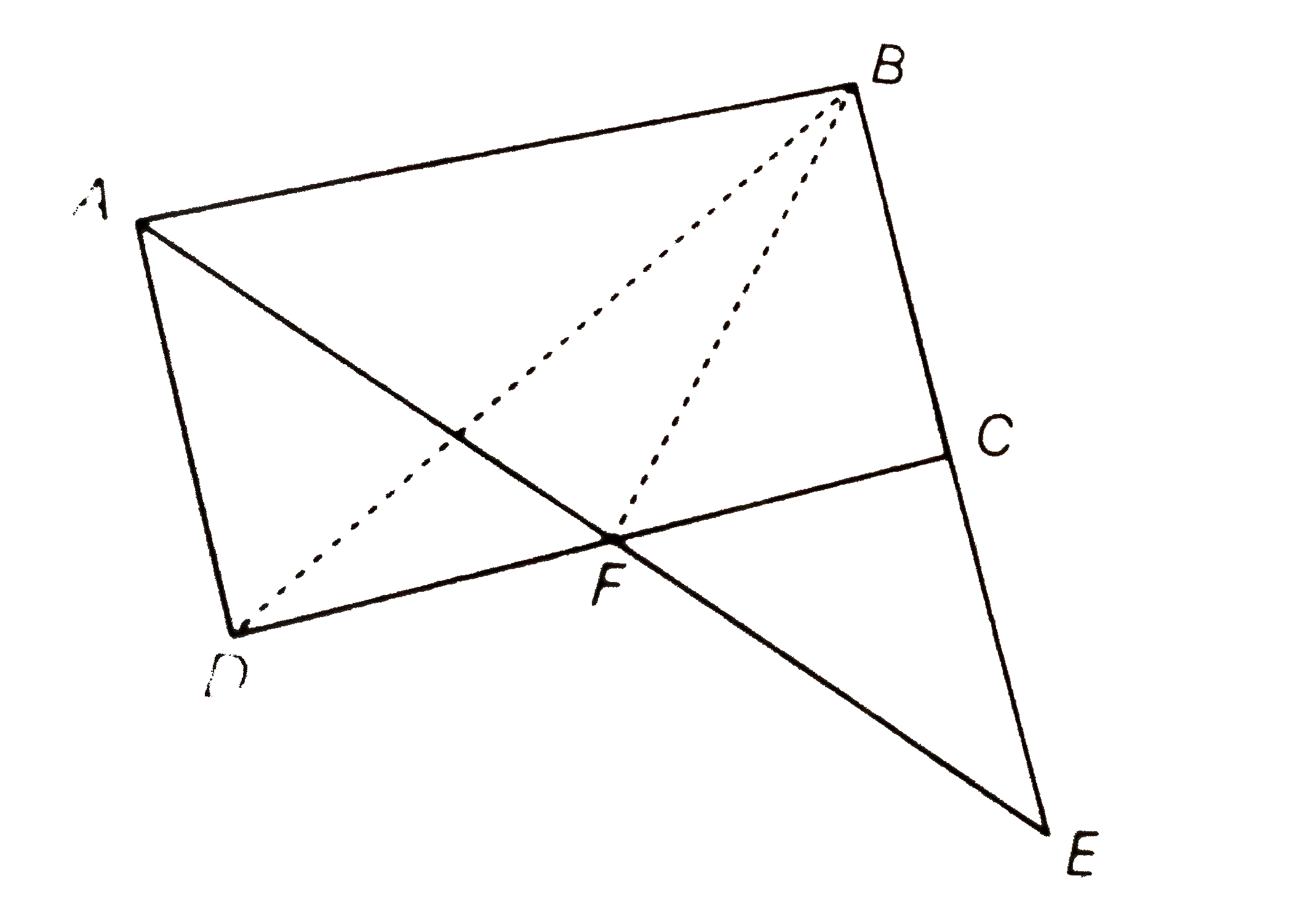
If ar(ΔDFB)=3cm2, then find the area of the parallelogram ABCD.
View SolutionThe locus of a point which divides the join of A(-1,1) and a variable point P on the circle x2+y2=4 in the ratio 3:2 is
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View Solution

